입출력 예시
number | limit | power | result |
5 | 3 | 2 | 10 |
10 | 3 | 2 | 21 |
나의 코드
import math
def solution(number, limit, power):
w_iron = []
for i in range(1, number+1):
count = 0
for j in range(1, int(math.sqrt(i))+1):
if i % j == 0:
count += 2
if i / j == j:
count -= 1
if count > limit:
w_iron.append(power)
break
else:
w_iron.append(count)
return sum(w_iron)
Python
복사
기억할 점
•
약수의 개수를 구하는 방법은 크게 3가지
1.
Naïve
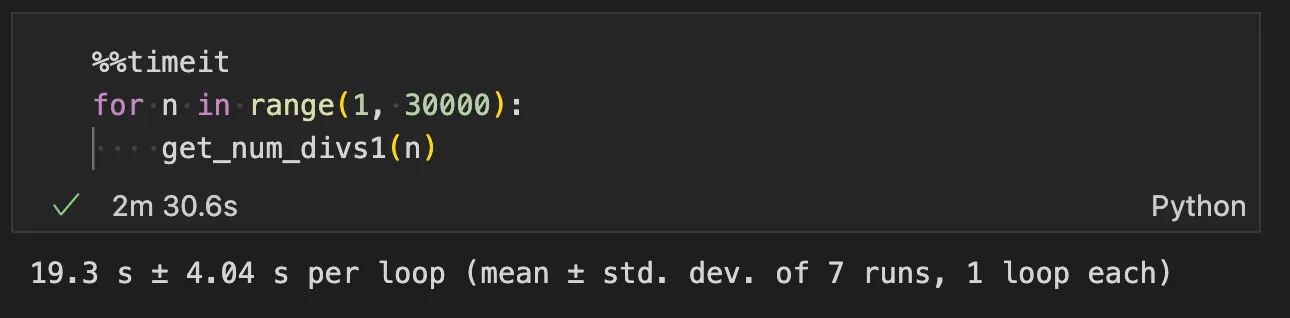
def get_num_divs1(n):
count = 0
for i in range(1, n+1):
if n % i == 0:
count += 1
return count
Python
복사
•
하나씩 센다 → 매우 오래 걸린다.
2.
제곱근 이용
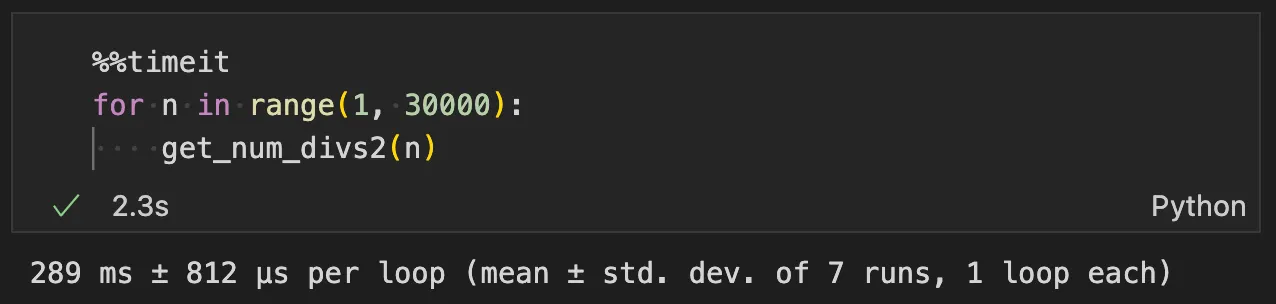
def get_num_divs2(n):
count = 0
for i in range(1, int(math.sqrt(n))+1):
if n % i == 0:
count += 2
if i * i == n:
count -= 1
return count
Python
복사
•
인수는 쌍(pair)으로 존재한다는 것을 이용한다.
•
n의 제곱근까지만 찾는다!
•
인수를 찾았다면, 그 인수의 짝이 있으므로 +2 를 해준다.
•
단, 만약 n이 어떤 수의 제곱이라면, +2를 해줄 경우 중복이 되므로, -1을 해준다.
3.
소인수 분해 이용
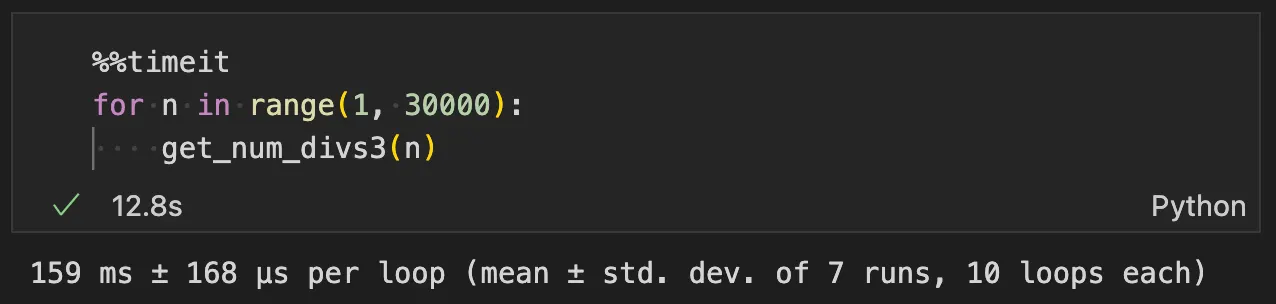
def get_num_divs3(n):
count = 1
for p in prime_factors(n):
count *= (p[1] + 1)
return count
def prime_factors(n):
factors = []
for i in range(2, int(math.sqrt(n))+1):
if n % i == 0: # 인수 i를 찾았다면
count = 0
while n % i == 0: # i로 나누어 떨어지는 동안
n //= i # n을 i로 나눈 몫을 n에 저장
count += 1 # 인수 i의 개수를 1 증가
factors.append((i, count))
if n > 1:
factors.append((n, 1))
return factors
Python
복사
•
a 어떤 수를 소인수분해 했을 때, 이라면, 인수의 갯수는 이다.
•
역시 인수는 제곱근까지만 찾아서 인수와 그 인수의 개수를 찾는다.
•
인수 를 찾았다면, 그 인수 로 안 나눠떨어질 때까지 을 나누고, 나눠떨어질 때마다 +1을 해준다.
속도는 1 << 2 < 3 순서로 빠르다. 소인수분해를 할 때도 제곱근을 사용하는 기법이 사용되므로, 적어도 제곱근 이용하는 방법은 기억하자!