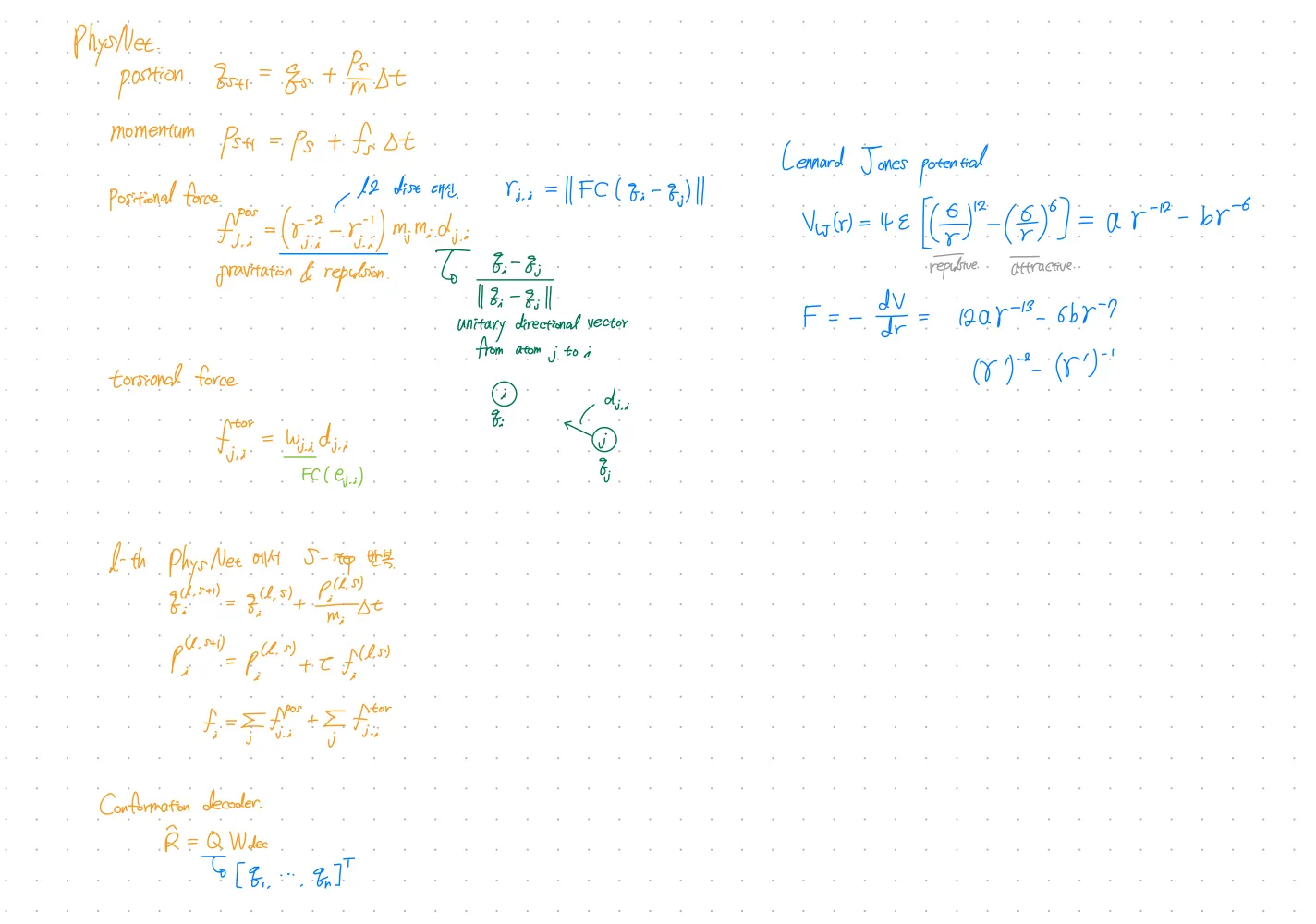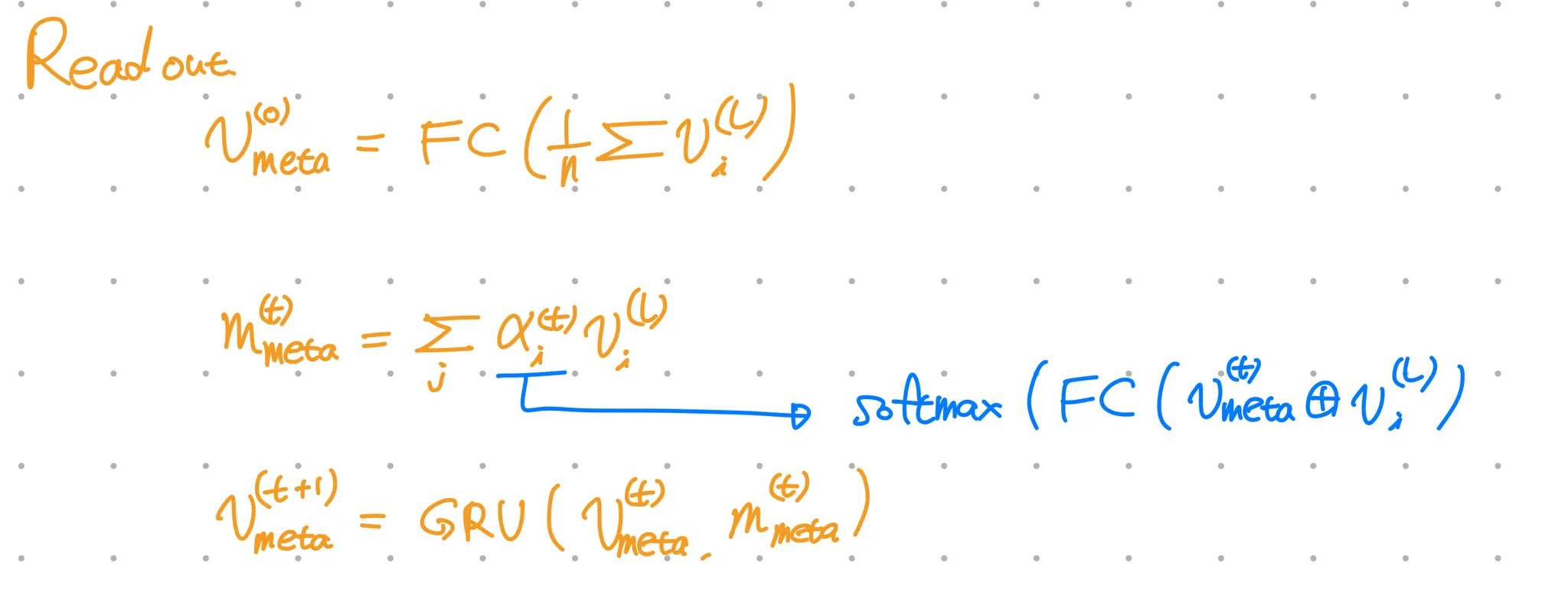Search

PhysChem: Deep Molecular Representation Learning via Fusing Physical and Chemical Information

•
NeurIPS 2021 Poster
•
OpenReview
https://openreview.net/forum?id=Uxi7X1EqywV&noteId=WA2nWkN6AjS

Summary

•
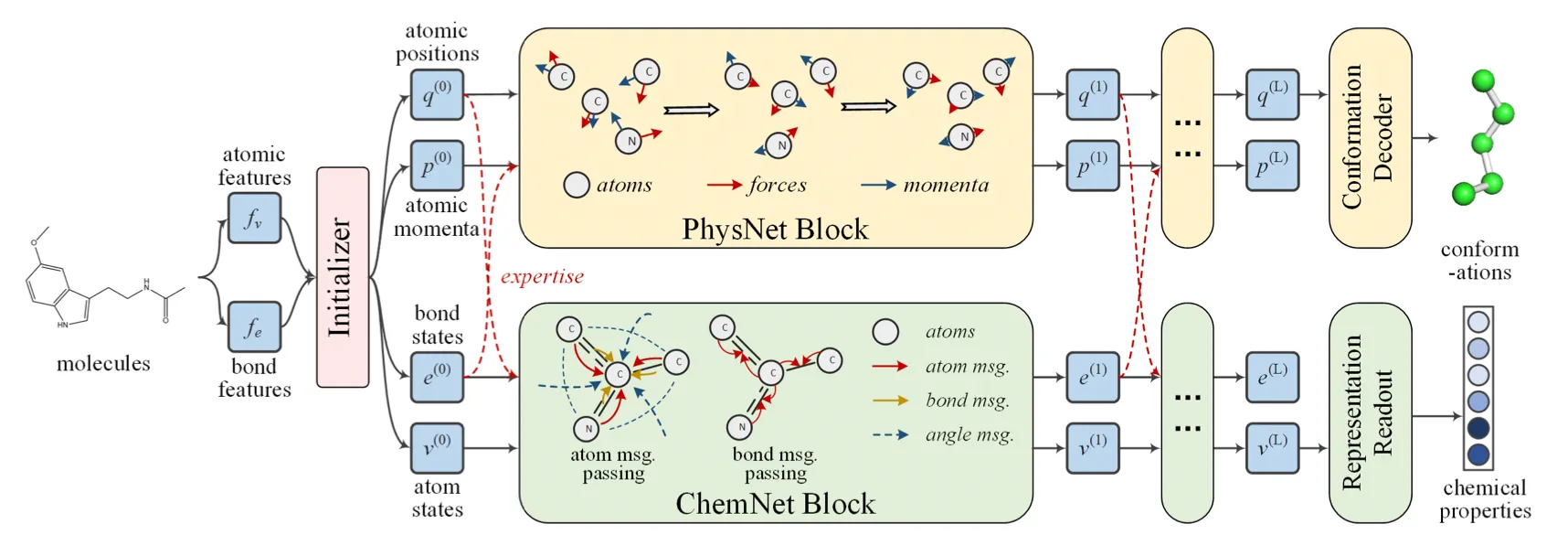
Used physicist network (PhysNet) and chemist network (ChemNet) simultaneously, and each network shares information to solve individual tasks.
•
PhysNet: Neural physical engine. Mimics molecular dynamics to predict conformation.
•
ChemNet: Message passing network for chemical & biomedical property prediction.
•
Molecule without 3D conformation can be inferred during test time.

Preliminaries

•
Molecular representation learning
Embedding molecules into latent space for downstream tasks.
•
Neural Physical Engines
Neural networks are capable of learning annotated potentials and forces in particle systems.
HamNet proposed a neural physical engine that operated on a generalized space, where positions and momentums of atoms were defined as high-dimensional vectors.
•
Multi-task learning
Sharing representations for different but related tasks.
•
Model fusion
Merging different models on identical tasks to improve performance.

Notation

•
Graph M=(V,E,n,m,Xv,Xe)\mathcal{M} = (\mathcal{V}, \mathcal{E}, n, m, \mathbf{X}^v, \mathbf{X}^e)
V\mathcal{V}: set of nn atoms
E\mathcal{E}: set of mm chemical bonds
Xv∈Rn×dv=(x1v,...,xnv)⊤\mathbf{X}^v \in \mathbb{R}^{n \times d_v} = (x^v_1, ..., x^v_n)^\top: matrix of atomic features
Xe∈Rm×de=(x1e,...,xme)⊤\mathbf{X}^e \in \mathbb{R}^{m \times d_e} = (x^e_1, ..., x^e_m)^\top: matrix of bond features

Model

•
Initializer
◦
Input: atomic features, bond features (from RDKit)
◦
Layer: fully connected layers
◦
Output:
▪
bond states, atom states for ChemNet
vi(0)=FC(xiv),i∈Vv^{(0)}_i = \text{FC}(x^v_i), i\in \mathcal{V}, ei,j(0)=FC(xi,je),(i,j)∈Ee^{(0)}_{i,j} = \text{FC}(x^e_{i,j}), (i, j)\in \mathcal{E}
▪
atom positions, atomic momenta for PhysNet
Bond strength adjacency matrix A(i,j)={0,if (i,j)∉EFCsigmoid(xi,je),if (i,j)∈EA(i,j)=\begin{cases}0, & \text{if $(i,j) \notin \mathcal{E}$}\\ \text{FC}_{\text{sigmoid}}(x^e_{i,j}), & \text{if $(i,j) \in \mathcal{E}$} \end{cases}
V~=GCN(A,V(0))\tilde{V} = \text{GCN}(A, V^{(0)})
{(qi(0)⊕pi(0))}=LSTM({v~i}),i∈V\{ (q^{(0)}_i \oplus p^{(0)}_i)\} = \text{LSTM}(\{\tilde{v}_i\}), i \in \mathcal{V}
•
PhysNet
◦
PhysNet is inspired by HamNet.
HamNet showed that neural networks can simulate molecular dynamics for conformation prediction.
◦
Directly parameterize the forces between each pair of atoms.
◦
Consider the effects of chemical interactions(e.g. bond types) by cooperating with ChemNet’s bond states.
◦
Introduces torsion forces.
◦
Output: 3D conformation
•
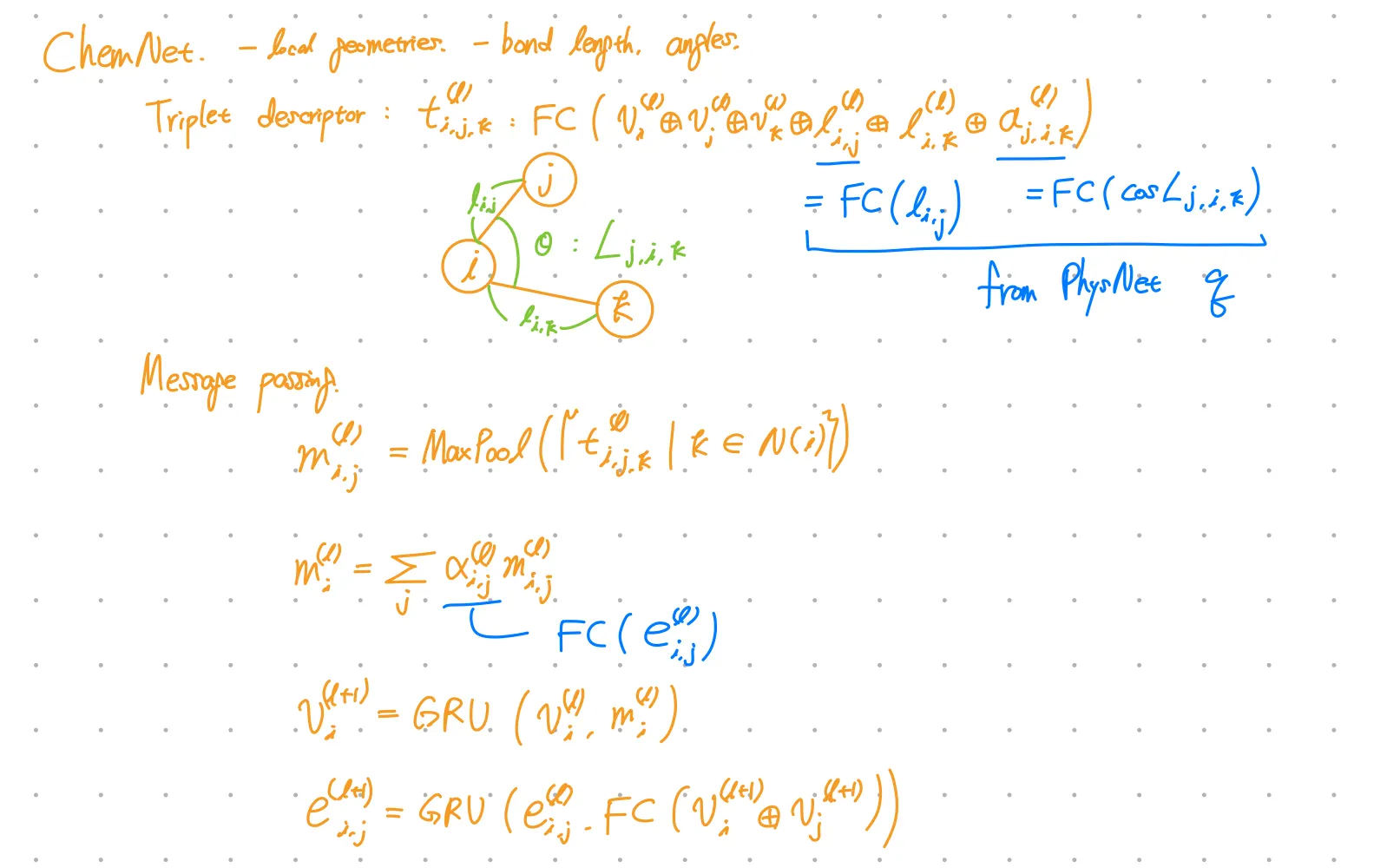
ChemNet
ChemNet modifies MPNN(message passing neural network) for molecular representation learning.
◦
Output: Molecule representation

Loss

•
LphysL_{\text{phys}}: Conn-k loss for Conformation prediction (PhysNet)
kk-hop connectivity loss
LConn−k(R^,R)=∥1nC^(k)⊙(D^−D)⊙(D^−D)∥FL_{\text{Conn}-k}(\hat{\mathbf{R}}, \mathbf{R}) = \|\frac{1}{n} \hat{\mathbf{C}}^{(k)} \odot (\hat{\mathbf{D}} - \mathbf{D}) \odot (\hat{\mathbf{D}} - \mathbf{D}) \|_{F}
⊙\odot: element-wise product
∥⋅∥\| \cdot \|: Frobenius norm
(D^−D)(\hat{\mathbf{D}} - \mathbf{D}) : distance matrix of the real and predicted conformations (R^−R)(\hat{\mathbf{R}} - \mathbf{R})
C^(k)\hat{\mathbf{C}}^{(k)}: normalized kk-hop connectivity matrix
•
LchemL_{\text{chem}}: MAE or Cross entropy loss for Property prediction (ChemNet)
•
Total loss
Ltotal=λLphys+LchemL_{\text{total}} = \lambda L_{\text{phys}} + L_{\text{chem}}
Checkpoints
•
Is Conn-k loss generally used in other conformation prediction models?
No! But seems related to local distance loss.
•
Is triplet descriptor generally used in other models?
No!