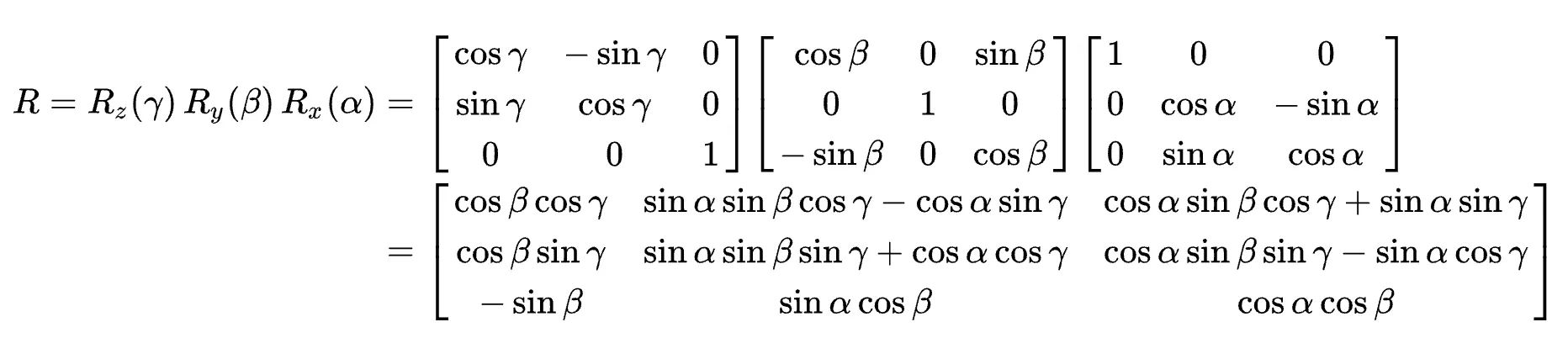1. Group (군)
어떤 set (집합)에 대해, 어떤 binary operation (이항연산)을 수행하여도 항상 그 set 안에 속하는 경우, 이 set과 binary operation의 묶음을 group이라고 한다.
Group을 이루기 위한 조건은 아래와 같다.
1.
Closure
2.
Associativity (결합법칙)
3.
Identity (항등원) 존재
4.
Inverse (역원)의 존재
Example of groups
•
Euclidean Groups
-차원 공간 상의 모든 rigid motion (translation, rotation, reflection) 의 집합은 group을 이룬다.
•
Special Euclidean Group
-차원 공간 상의 translation과 rotation
•
Orthogonal Group
-차원 공간 상의 rotation과 reflection
•
Special Orthogonal Group
-차원 공간 상의 rotation
2. Linear map
Rigid motion은 linear mapping 이고, linear map은 matrix 형태로 표현할 수 있다.
예를 들어, 3차원 상에서 rotation matrix는 아래와 같이 표현한다.
x축을 중심으로 만큼, y축을 중심으로 만큼, z축을 중심으로 만큼 회전
3. Invariance & Equivariance
어떤 operation 이자 group 에 대해,
•
-invariant
•
-equivariant
즉, invariance 는 equivariance의 special case (를 만족하는) 이다.
우리가 원하는 -equivariant 한 함수 는 어떻게 만들까?
그 전에, vector space에 대해 잠시 복습해보자.
4. Vector Space
Linear algebra에서 배웠듯이, 모든 vector space는 basis를 가진다.
예를 들어, 의 경우, 은 basis 이다. 또, 도 basis 이다. 즉, vector space 상의 임의의 점을 이 basis 의 조합으로 항상 표현할 수 있다.
그런데 만약 vector space 가 함수들의 집합인 경우에는 어떨까? 그 집합에 속하는 임의의 함수를 basis로 구분하여 나타낼 수 있는 방법이 있을까?
5. Fourier Series
Periodic functions can be expressed as a sum of trigonometric functions.
임의의 함수를 삼각함수 또는 지수함수의 일차결합으로 나타내는 것을 의미한다.
더 formal 하게 정의해보면,
에 대해, 인 임의의 에 대해
→ 즉, 의 basis는 이다.
참고: 은 one-dimensional sphere, 즉 circle 이다.
6. Laplace Series
Fourier series를 로 연장하여 Laplace series를 정의해보자.
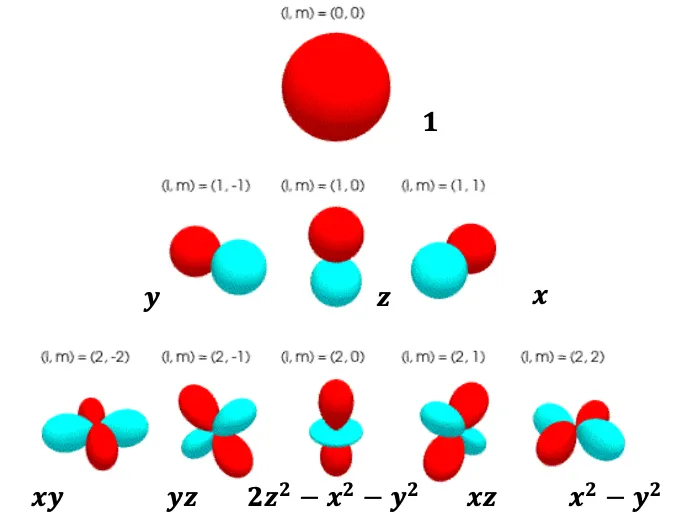
에 대해, 인 임의의 에 대해
→ 즉, 의 basis는 이다.
이때, .
참고: 는 unit sphere 이다.
이제 순으로 equivariance 를 확장시켜 나가보자.
7. -equivariance
Vector space 에 작용하는 에 대해 를 아래와 같이 정의하면, equivariant한 를 얻을 수 있다.
이때, 이다.
은 차원의 matrix이고, 아래의 중요한 성질을 가진다.
이때, 이다.
를 만족하면, equivariance 를 만족한다고 할 수 있다.
이때 은 -irreps (irreducible representation)라고 부르고, , 즉 등으로 표현한다.
예를 들어보자. 에 대해,
•
, 이라고 정의하면,
◦
◦
이므로, equivariant function 와 을 얻었다.
7.1. More equivariant functions
그렇다면 등 더 많은 equivariant function은 어떻게 얻을 수 있을까?
아래 세 operation을 통해 얻을 수 있다.
•
Composition
•
Linear sum
•
◦
◦
두 함수를 조합하여 어떤 함수 를 얻을 수 있다. 이때, 이다.
예시
7.2. Learnable parameter
이제 여러 -equivariant function을 얻을 수 있다는 것은 확인했다.
그럼 neural network의 핵심인 learnable parameter는 어떻게 추가할 수 있을까?
각 irreps 에 scalar weight를 곱해주면 된다.
예를 들어, 로 정의하고 이때 는 이고 은 라고 해보자.
이를 ”2x1e”, ”1x0e + 1x1e” 라고 표기한다.
그리고 output을 이라고 정의하면, 총 4개의 learnable parameter가 있다.
•
과 , 그리고 와 를 조합하면 0e, 1e, 2e 가 가능한데, 으로 표시하였으므로 그 중 0e에 해당하는 것만 사용한다는 의미이다. 따라서 의 첫 번째 원소는 0e 이다.
•
과 , 와 을 조합하면 1e만 가능하다.
•
따라서 는 “1x0e + 1x1e” 로 표기할 수 있다.
7.3. Non-linearity
그럼 non-linearity는 어떻게 부여할까?
대부분의 non-linear function은 그 결과값이 equivariance를 유지하지 못 하는 경우가 많으므로, non-linear function에 들어가는 input으로는 invariant한 function만 넣어주어야 한다.
따라서, 방금 전 예시에서 의 0e 부분인 에 sigmoid 등을 붙인 로 non-linearity 를 부여할 수 있다. 1e, 2e 등 다른 것들은 equivariant 하지만 invariant 하지는 않아서 non-linearity 를 부여하면 equivariance 성질을 잃게 된다.
최종적으로 우리가 원하는 feature는 invariant 한 형태가 대부분일텐데, 처음부터 invariant한 연산만 수행하면 가능한 연산이 너무 제한적이기 때문에 equivariant 연산들로 neural net을 구성하고, 마지막에 invariant feature를 얻도록 하는 방향이라고 이해하면 된다.
-equivariance
앞서 본 -equivariance 를 만족하는 연산과 적절한 parametrization과 non-linearity 가 만족되는 네트워크를 여러 층 쌓으면 -equivariant neural network를 만들 수 있다.
는 에 translation 연산이 추가된 개념인데, 이는 각 -equivariant layer에 input을 normalized relative vector (아래 수식 참고) 형태로 넣어주게 되면 만족할 수 있다.
-equivariance
-equivariance 는 에 reflection 연산이 추가된 개념이다. 이는 parity=라는 개념을 도입하여 확장할 수 있다.
Parity는 쉽게 말해 어떤 object가 홀수인지, 짝수인지를 나타내는 개념이라고 봐도 될 것 같다.