Search

DiffDock (english)

Table of Contents
•
This article is one of the first research work that formulated molecular docking as a generative problem.
•
Showed very interesting results with decent performance gain.
•
If you are interested in molecular docking and diffusion models, this is definitely a must-read paper!
•
It is highly recommended to watch youtube video explained by the authors.

Summary

•
Molecular docking as a generative problem, not regression!
◦
Problem of learning a distribution over ligand poses conditioned on the target protein structure p(x∣y)p(\mathbf{x} | \mathbf{y})
•
Used “Diffusion process” for generation
•
Two separate model
◦
Score model: s(x,y,t)s(\mathbf{x}, \mathbf{y}, t)
Predicts score based on ligand pose x\mathbf{x}, protein structure y\mathbf{y}, and timestep tt
◦
Confidence model: d(x,y)d(\mathbf{x}, \mathbf{y})
Predicts whether the ligand pose has RMSD below 2Å compared to ground truth ligand pose
•
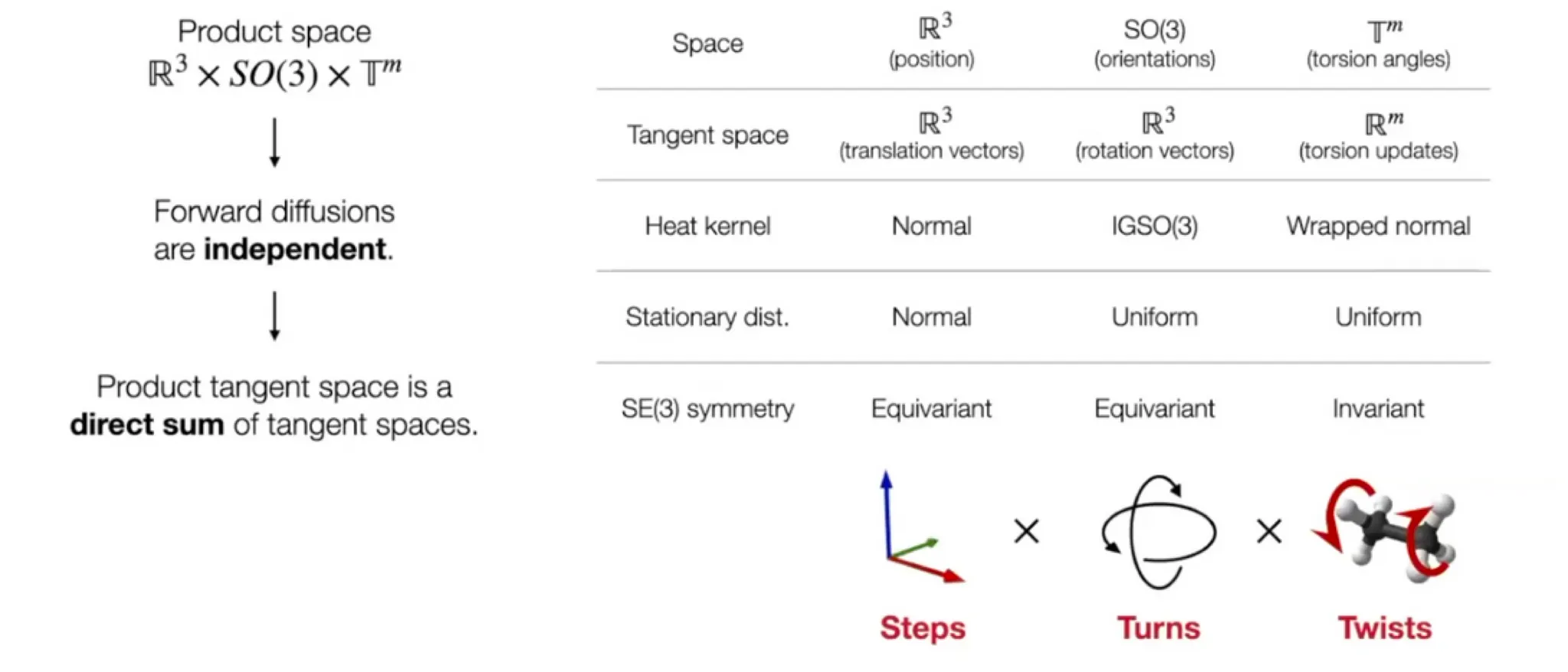
Diffusion on Product space P\mathbb{P}
◦
Reduced degrees of freedom 3n→(m+6)3n \rightarrow (m+6)

Preliminaries

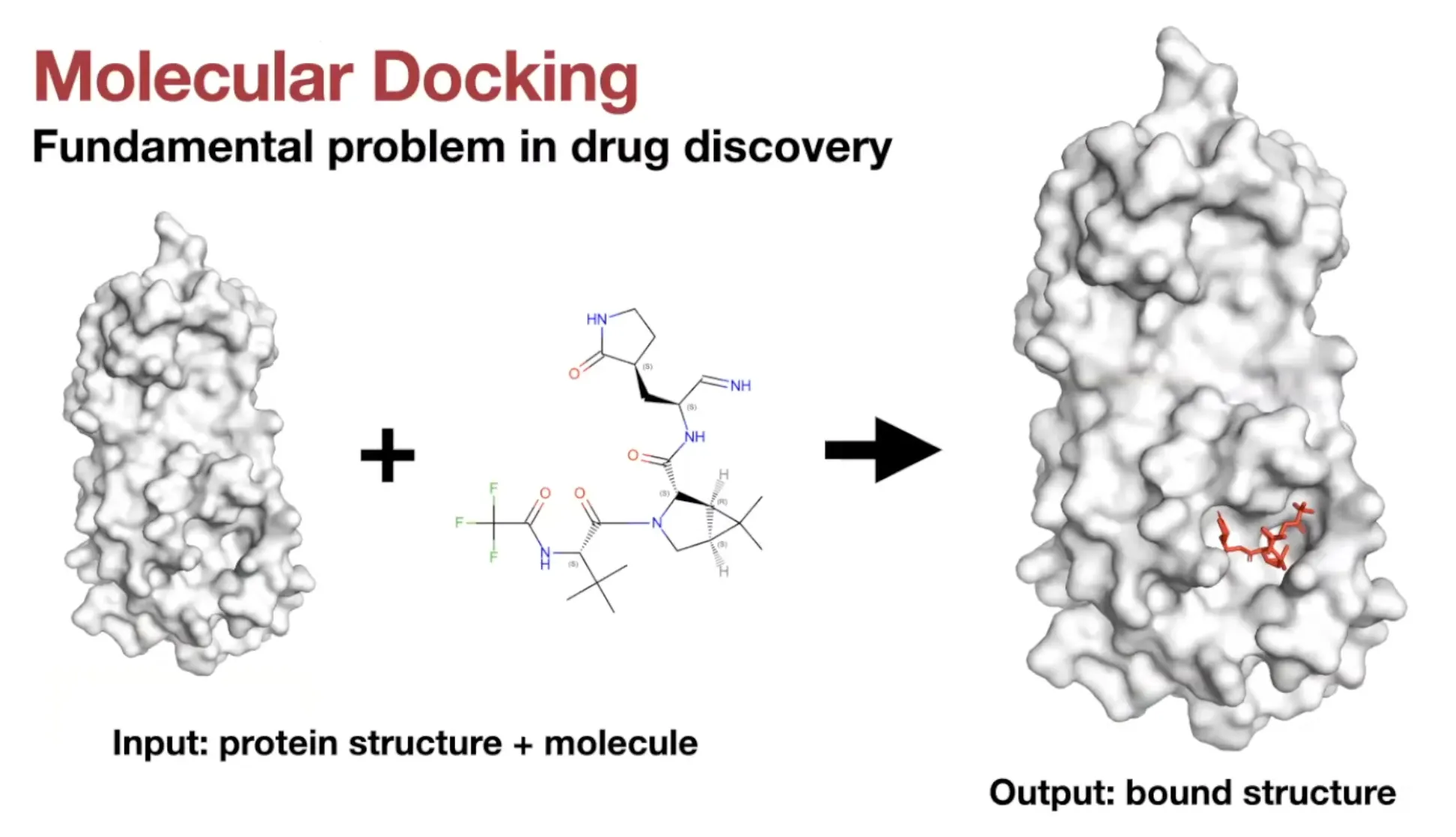
Molecular Docking

•
Definition:
Predicting the position, orientation, and conformation of a ligand when bound to a target protein
•
Two types of tasks
◦
Known-pocket docking
▪
Given: position of the binding pocket
◦
Blind docking
▪
More general setting: no prior knowledge about binding pocket

Previous works: Search-based / Regression-based

•
Search based docking methods
◦
Traditional methods
◦
Consist of parameterized physics-based scoring function and a search algorithm
◦
Scoring function
▪
Input: 3D structures
▪
Output: estimate of the quality/likelihood of the given pose
◦
Search algorithm
▪
Stochastically modifies the ligand pose (position, orientation, torsion angles)
▪
Goal: finding the global optimum of the scoring function.
◦
ML has been applied to parameterize the scoring function.
▪
But very computationally expensive (large search space)
◦
Example
•
Regression based methods
◦
Recent deep learning method
◦
Significant speedup compared to search based methods
◦
No improvements in accuracy
◦
Example
▪
•
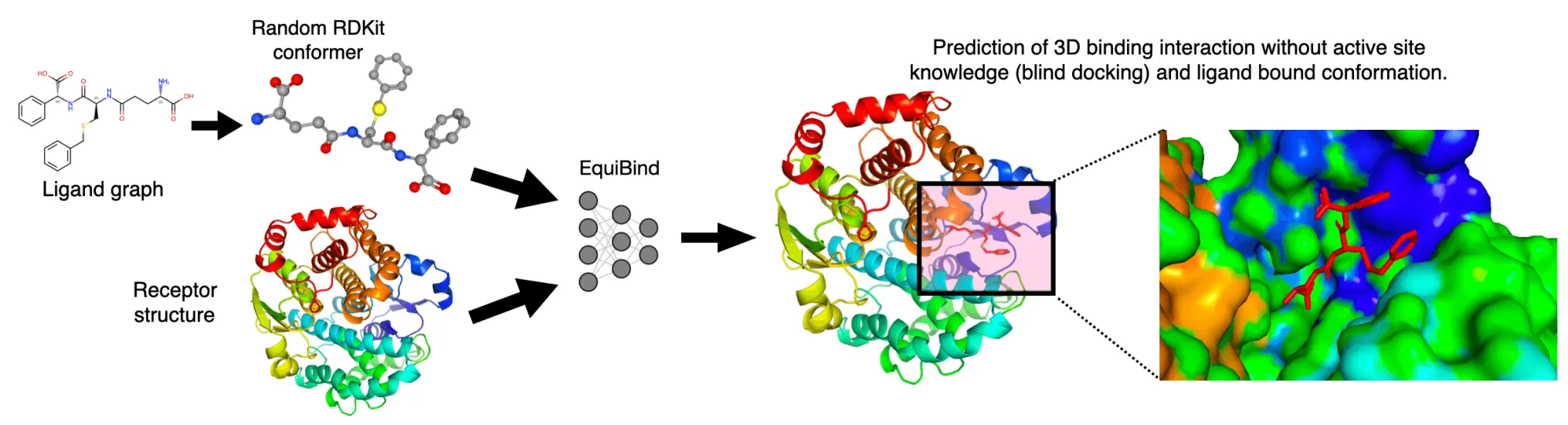
Tried to tackle the blind docking task as a regression problem by directly predicting pocket keypoints on both ligand and protein and aligning them.
▪
•
Improved over this by independently predicting a docking pose for each possible pocket and then ranking them.
▪
•
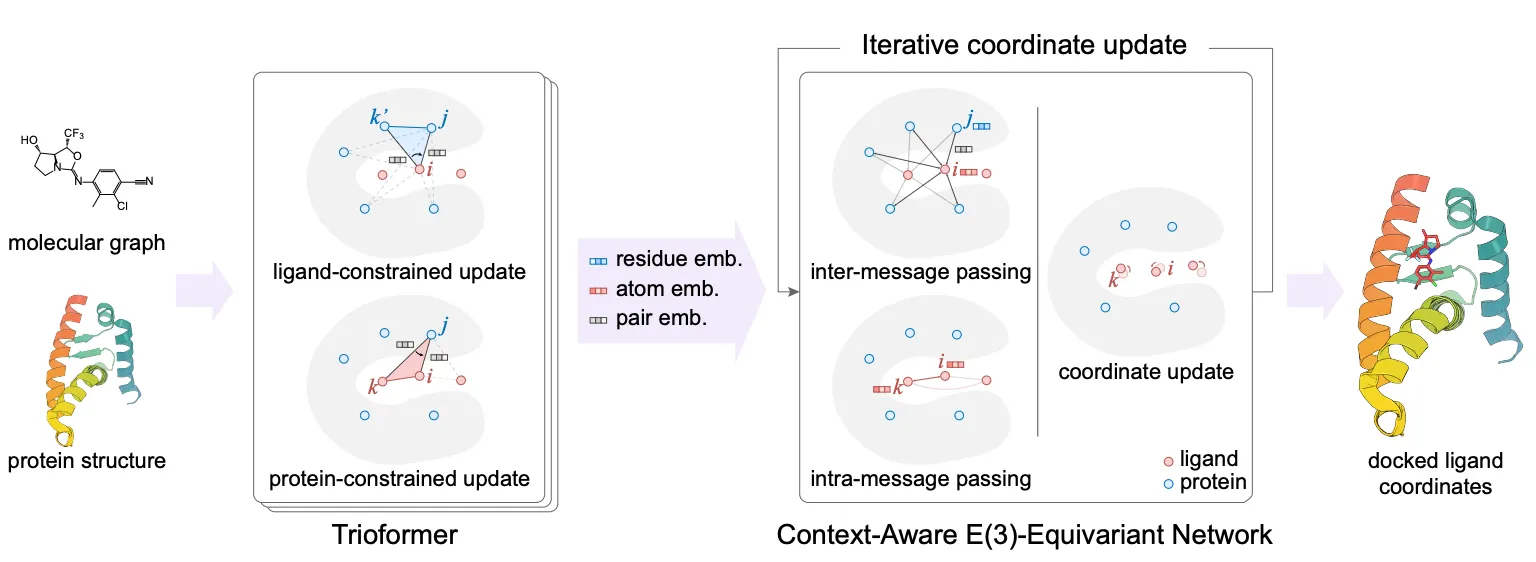
Used ligand-constrained & protein-constrained update layer to embed ligand atoms and iteratively updated coordinates.

Docking objective

•
Standard evaluation metric:
◦
Lϵ=∑x,yIRMSD(y,y^(x))<ϵ\mathcal{L}_\epsilon = \sum_{x, y} I_{\text{RMSD}(y, \hat{y}(x))<\epsilon}: proportion of predictions with RMSD<ϵ\text{RMSD} < \epsilon → Not differentiable!
◦
Instead, we use argminy^lim⁡ϵ→0Lϵ\text{argmin}_{\hat{y}} \lim_{\epsilon \rightarrow 0} \mathcal{L}_\epsilon as objective function.
•
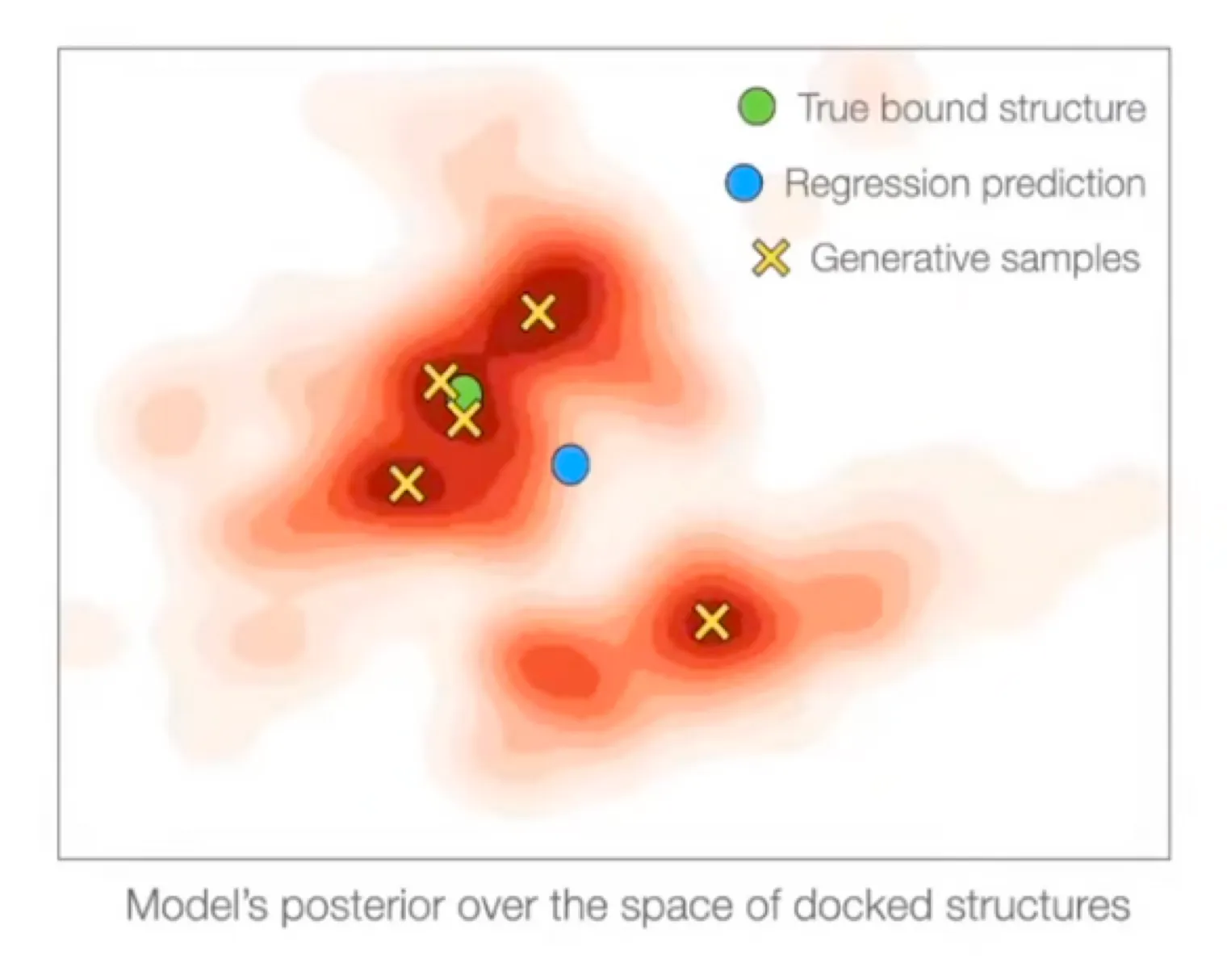
Regression is suitable for docking only if it is unimodal.
•
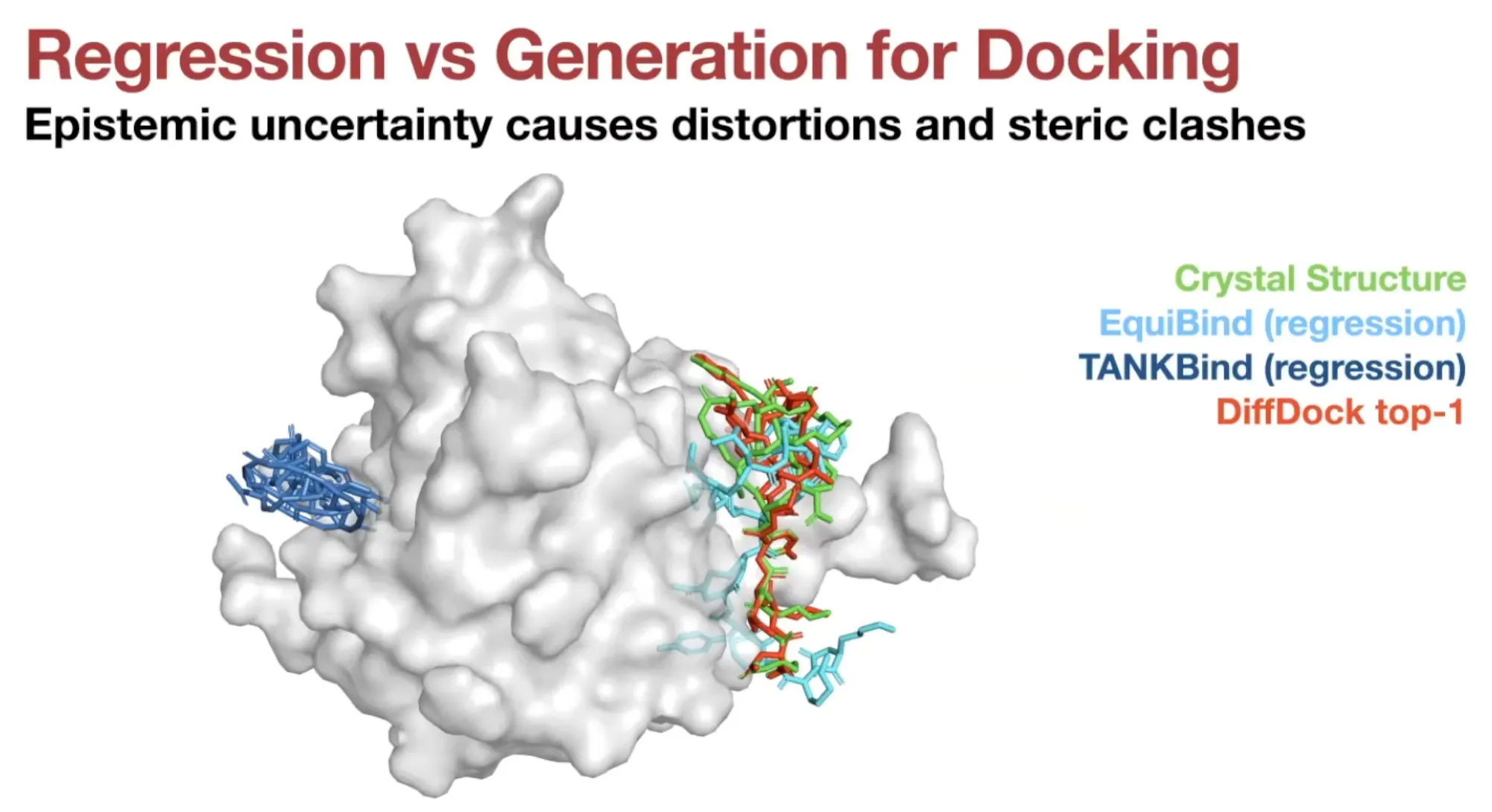
Docking has significant aleatoric (irreducible) & epistemic (reducible) uncertainty
◦
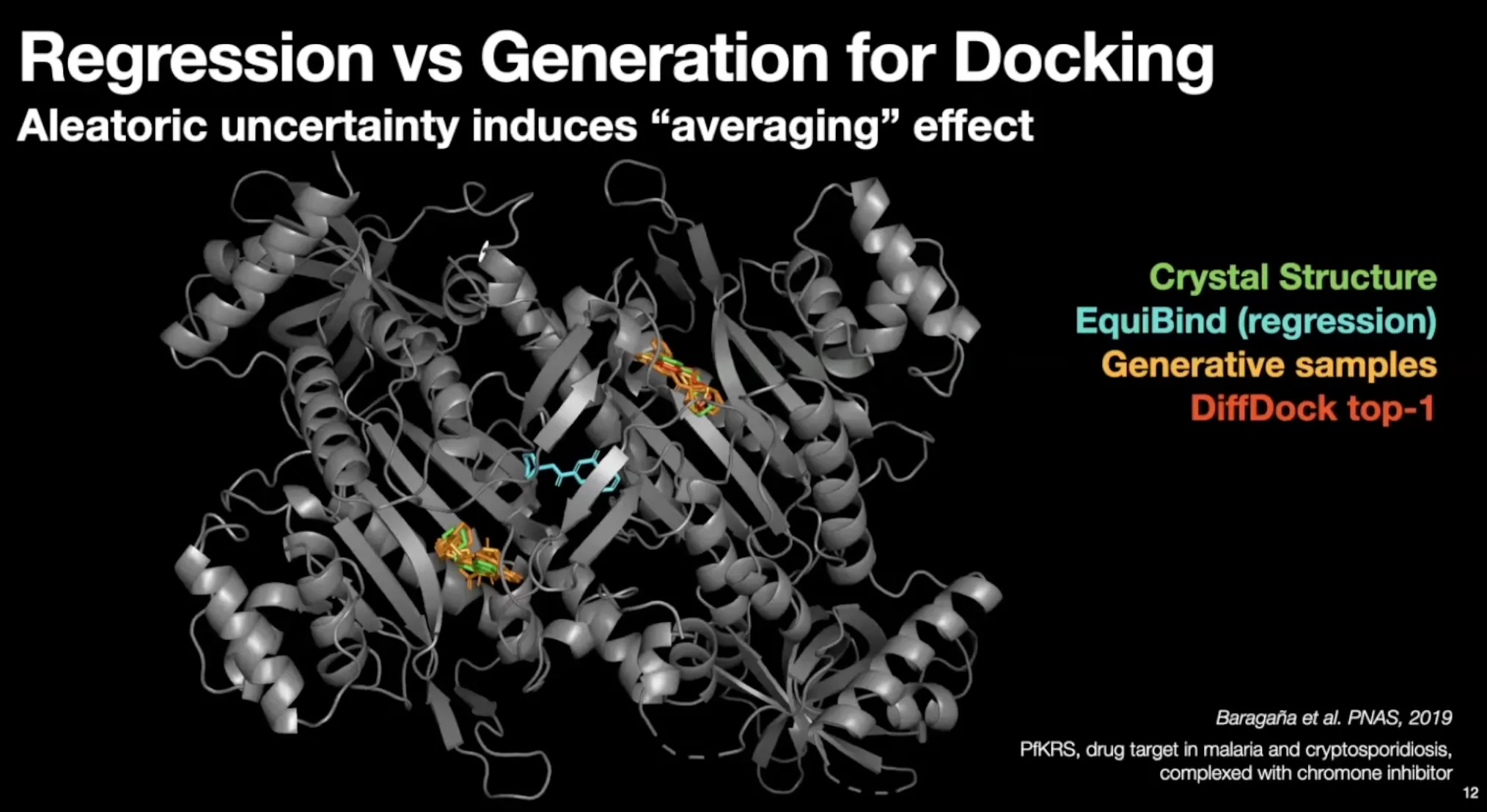
Regression methods will minimize ∑∥y−y^∥22\sum \|y - \hat{y}\|^2_2 → will produce weighted mean of multiple modes
◦
On the other hand, generative model will populate all/most modes!
•
Regression (EquiBind) model set conformer in the middle of the modes.
•
Generative samples can populate conformer in most modes.
•
Much less steric clashes for generative models

Diffusion Model

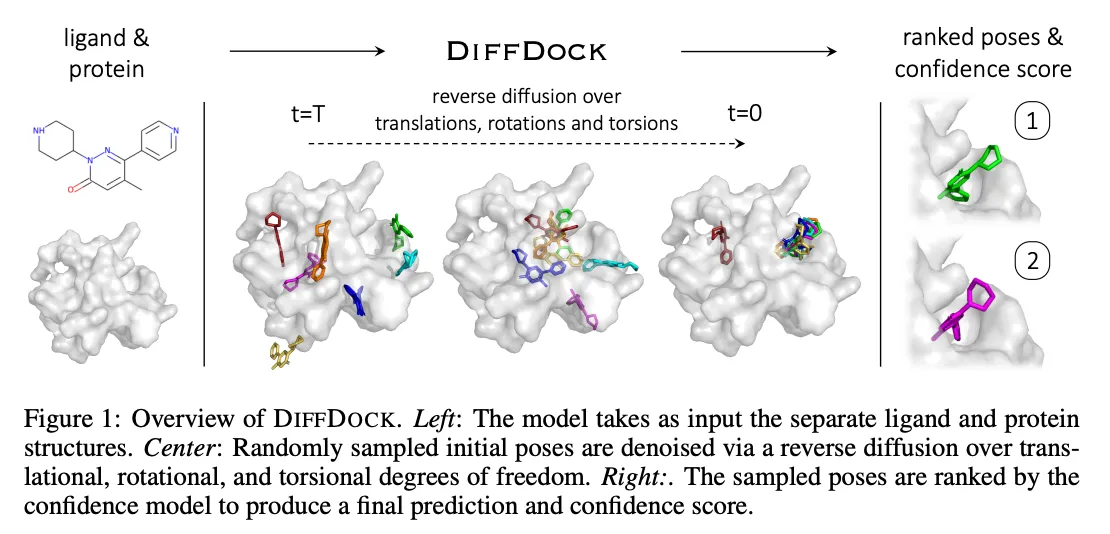
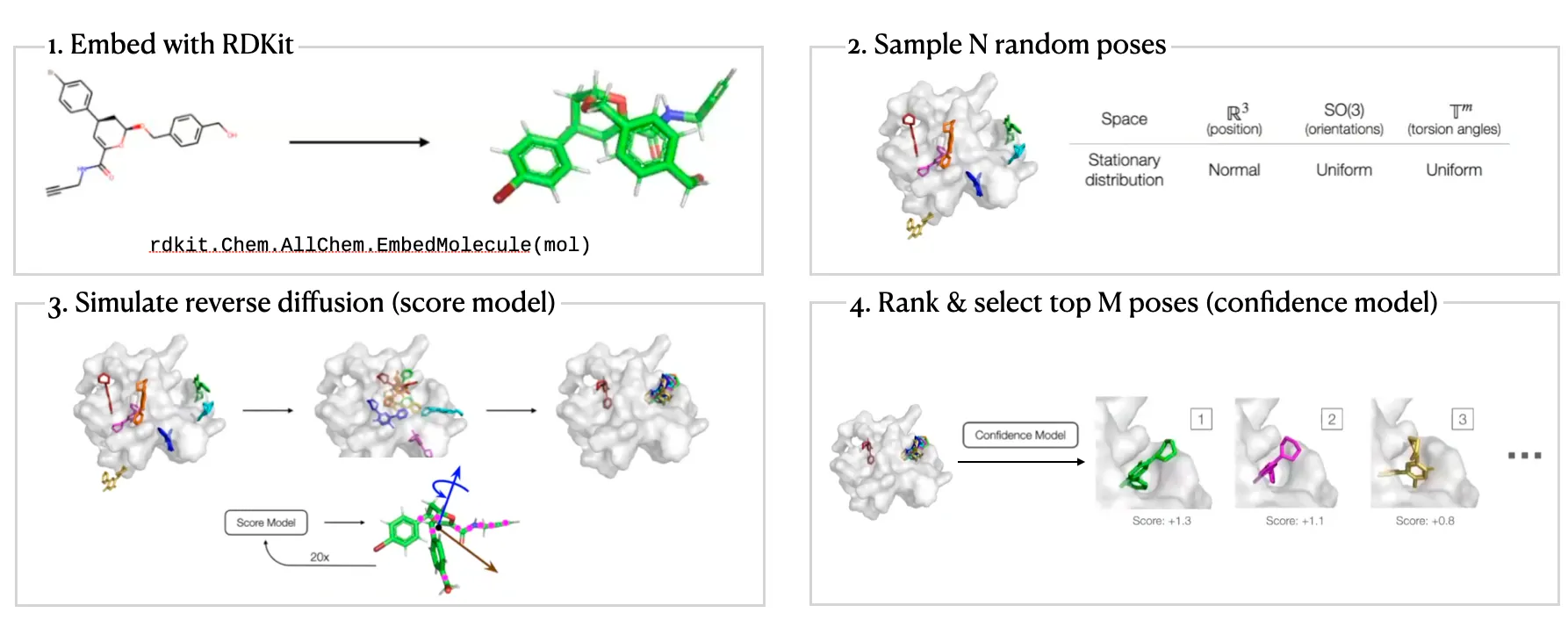
DiffDock Overview

•
Two-step approach
◦
Score model: Reverse diffusion over translation, rotation, and torsion
◦
Confidence model: Predict whether or not each ligand pose is RMSD<2A˚\text{RMSD} < 2\text{Å} compared to ground truth ligand pose

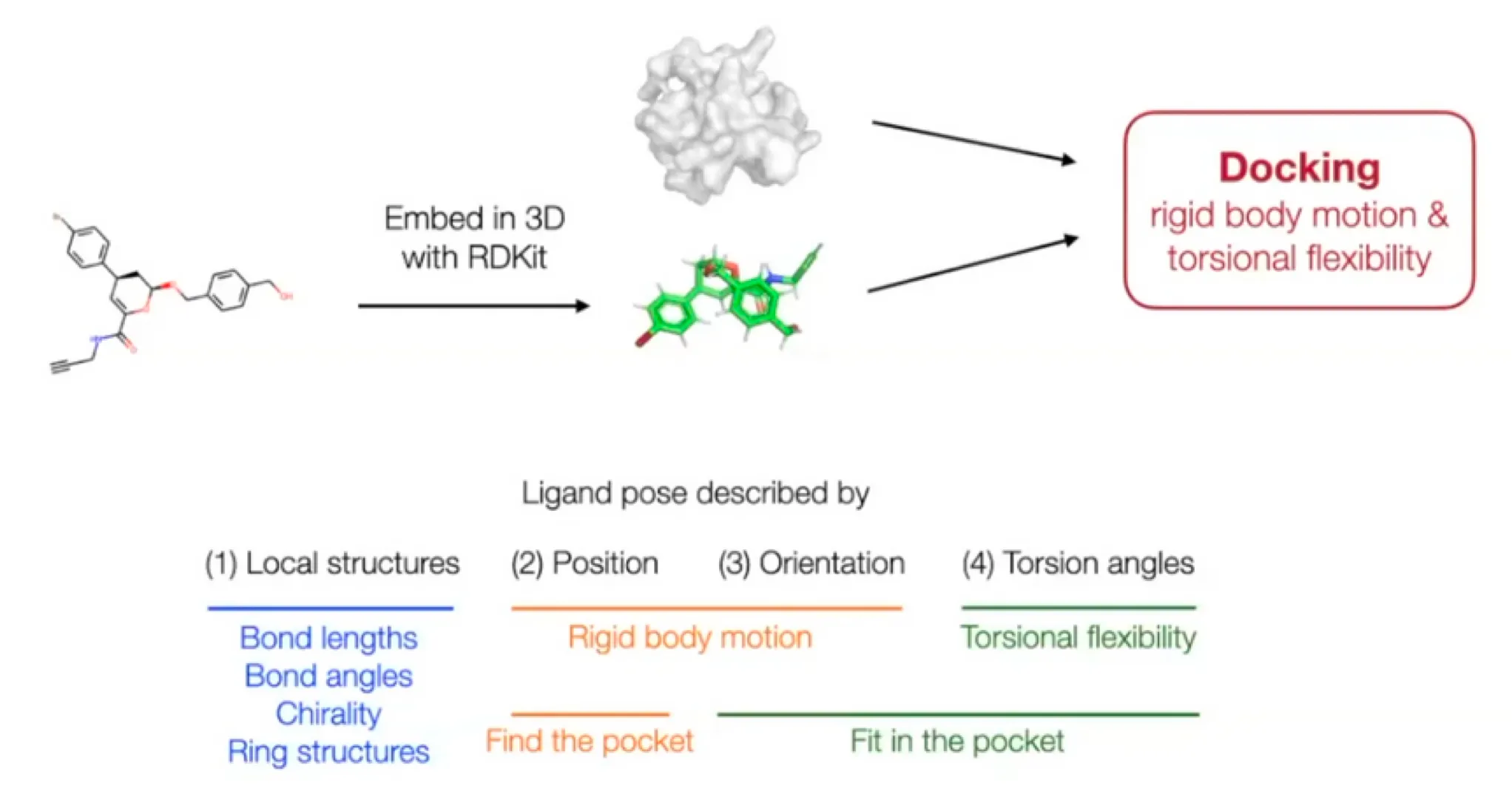
Score model

•
Ligand pose: R3n\mathbb{R}^{3n} (nn: number of atoms)
•
But molecular docking needs far less degrees of freedom.
◦
Reduced degree of freedom: (m+6)(m+6)
▪
Local structure: Fixed (rigid) after conformer generation with RDKit EmbedMolecule(mol)
•
Bond length, angles, small rings
▪
Position (translation): R3\mathbb{R}^3 - 3D vector
▪
Orientation (rotation): SO(3)SO(3) - three Euler angle vector
▪
Torsion angles: Tm\mathbb{T}^m (mm: number of rotatable bonds)
◦
Can perform diffusion on product space P:R3×SO(3)×Tm\mathbb{P}: \mathbb{R}^3 \times SO(3) \times \mathbb{T}^m
▪
For a given seed conformation c\mathbf{c}, the map A(⋅,c):P→McA(\cdot, \mathbf{c}): \mathbb{P} \rightarrow \mathcal{M}_\mathbf{c} is a bijection!

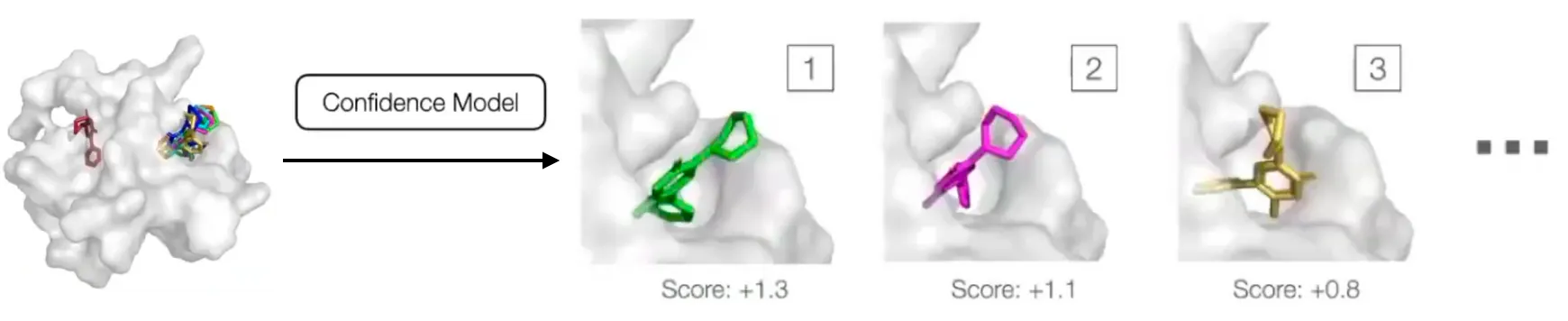
Confidence Model

•
Generative model can sample an arbitrary number of poses, but researchers are interested in one or a fixed number of them.
•
Confidence predictions are very useful for downstream tasks.
•
Confidence model d(x,y)d(\mathbf{x}, \mathbf{y})
◦
x\mathbf{x}: pose of a ligand
◦
y\mathbf{y}: target protein structure
•
Samples are ranked by score and the score of the best is used as overall confidence score.
•
Training & Inference
◦
Ran the trained diffusion model to obtain a set of candidate poses for every training example and generate binary labels: each pose has RMSD below 2A˚2 \text{Å} or not.
◦
Then the confidence model is trained with cross entropy loss to predict the binary label for each pose.
◦
During inference, diffusion model is run to generate NN poses in parallel, and passed to the confidence model that ranks them based on its confidence that they have RMSD below 2A˚2\text{Å}.

DiffDock Workflow

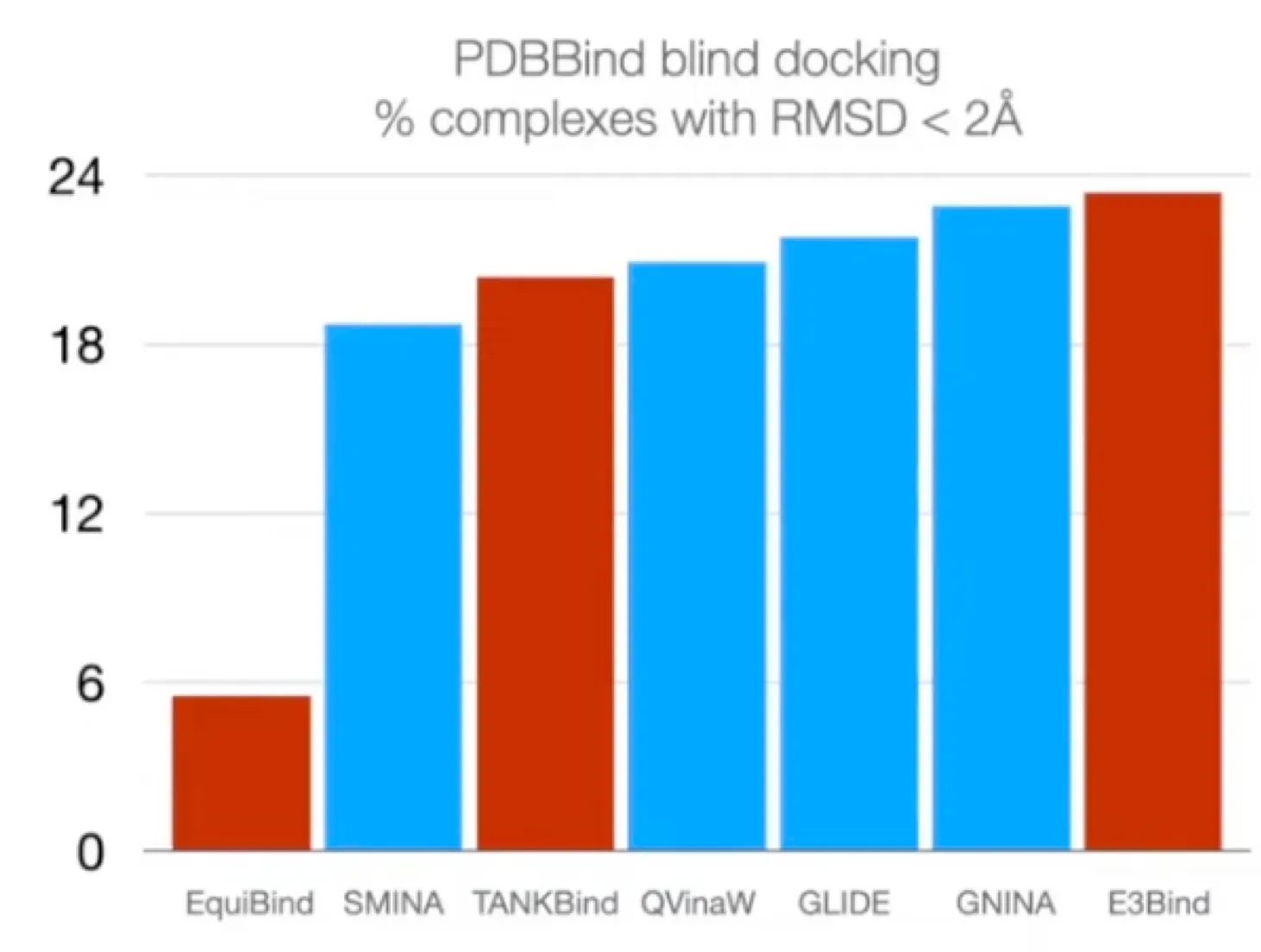
DiffDock Results

Personal opinions

•
It is impressive that the authors formulated molecular docking as a generative problem, conditioned on protein structure.
•
But it is not an end-to-end approach. And there are some discrepancy between the inputs and output of the confidence model. The input is the predicted ligand pose x^\hat{\mathbf{x}} and protein structure y\mathbf{y}, but the output is “whether the RMSE is below 2Å between predicted ligand pose x^\hat{\mathbf{x}} and ground truth ligand pose x\mathbf{x}”.
•
There are quite a room to improve the performance, but it requires heavy workloads of GPUs.
•
I’m skeptical about the generalizability of this model since there are almost no physics informed inductive bias in the model.

Reference

•
Blog
Generative Modeling by Estimating Gradients of the Data Distribution | Yang Song
This blog post focuses on a promising new direction for generative modeling. We can learn score functions (gradients of log probability density functions) on a large number of noise-perturbed data distributions, then generate samples with Langevin-type sampling. The resulting generative models, often called <em>score-based generative models</em>, has several important advantages over existing model families: GAN-level sample quality without adversarial training, flexible model architectures, exact log-likelihood computation, and inverse problem solving without re-training models. In this blog post, we will show you in more detail the intuition, basic concepts, and potential applications of score-based generative models.
https://yang-song.net/blog/2021/score/
What are Diffusion Models?
[Updated on 2021-09-19: Highly recommend this blog post on score-based generative modeling by Yang Song (author of several key papers in the references)]. [Updated on 2022-08-27: Added classifier-free guidance, GLIDE, unCLIP and Imagen. [Updated on 2022-08-31: Added latent diffusion model. So far, I’ve written about three types of generative models, GAN, VAE, and Flow-based models. They have shown great success in generating high-quality samples, but each has some limitations of its own.
https://lilianweng.github.io/posts/2021-07-11-diffusion-models/