Search
Duplicate

Set Transformer: A framework for attention-based permutation-invariant neural networks

Set Transformer: A Framework for Attention-based Permutation-Invariant Neural Networks
Many machine learning tasks such as multiple instance learning, 3D shape recognition, and few-shot image classification are defined on sets of instances. Since solutions to such problems do not depend on the order of elements of the set, models used to address them should be permutation invariant.
https://arxiv.org/abs/1810.00825
ICML (2019), cited over 300 times

1. Introduction

Many ML tasks are defined on sets of instances.
→ These tasks do not depend on the order of elements
→ We need permutation invariant models for these tasks

2. Major contribution

Set Transformer
•
Used self-attention to encode every element in a set.
→ Able to encode pairwise- or higher-order interactions.
•
Authors introduced an efficient attention scheme inspired by inducing point methods from sparse Gaussian process literature.
→ Reduced the O(n2)\mathcal{O}(n^2) computation to O(nm)\mathcal{O}(nm)
•
Used self-attention to aggregate features
→ Beneficial when the problem requires multiple outputs that depend on each other
e.g.) meta-clustering

3. Background

Set-input problems?

Definition: A set of instances is given as an input and the corresponding target is a label for the entire set.
e.g.) 3D shape recognition, few shot image classification
Requirements for a model for set-input problems
•
Permutation invariance = order-independent
•
Input size invariance
c.f.) Ordinary MLP or RNNs violate these requirements.
Recent works
[Edwards & Storkey (2017)], [Zaheer et al. (2017)] proposed set pooling methods.
Framework
1.
Each element in a set is independently fed into a feed-forward neural network.
2.
The resulting embeddings are then aggregated using a pooling operation(mean, max, sum...)
→ this framework is proven to be a universal approximator for any set function.
→ However, it fails to learn complex mappings & interactions between elements in a set
e.g.) amortized clustering problem
Google search
Amortized clustering: Reusing the previous inference (clustering) results to accelerate the inference (clustering) of new dataset.

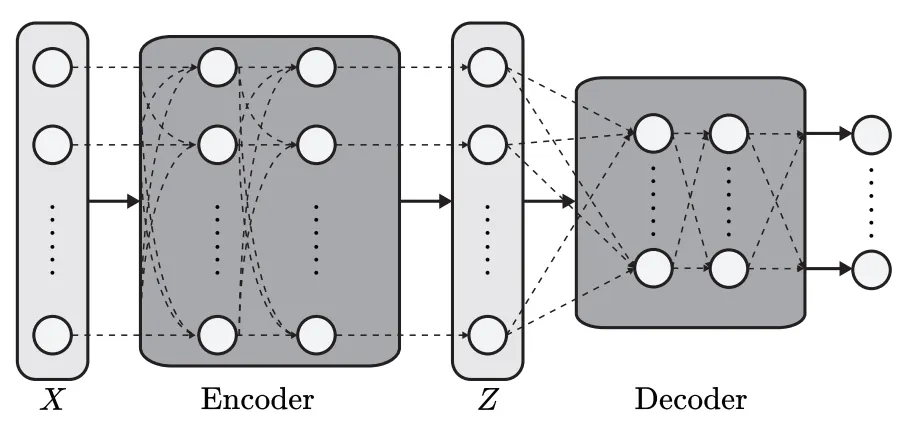
Pooling architecture for sets

Universal representation of permutation invariant functions
net({x1,...,xn})=ρ(pool({ϕ(x1),...,ϕ(xn)}))\text{net}(\{x_1,...,x_n\}) = \rho (\text{pool}(\{\phi(x_1),...,\phi(x_n)\}))
ϕ:encoder; ρ:decoder\phi: \text{encoder; } \rho: \text{decoder}
The model remains permutation-invariant even if the "encoder" ϕ\phi is a stack of permutation-equivariant(order-dependent) layers
e.g.) permutation-equivariant layer - order matters!
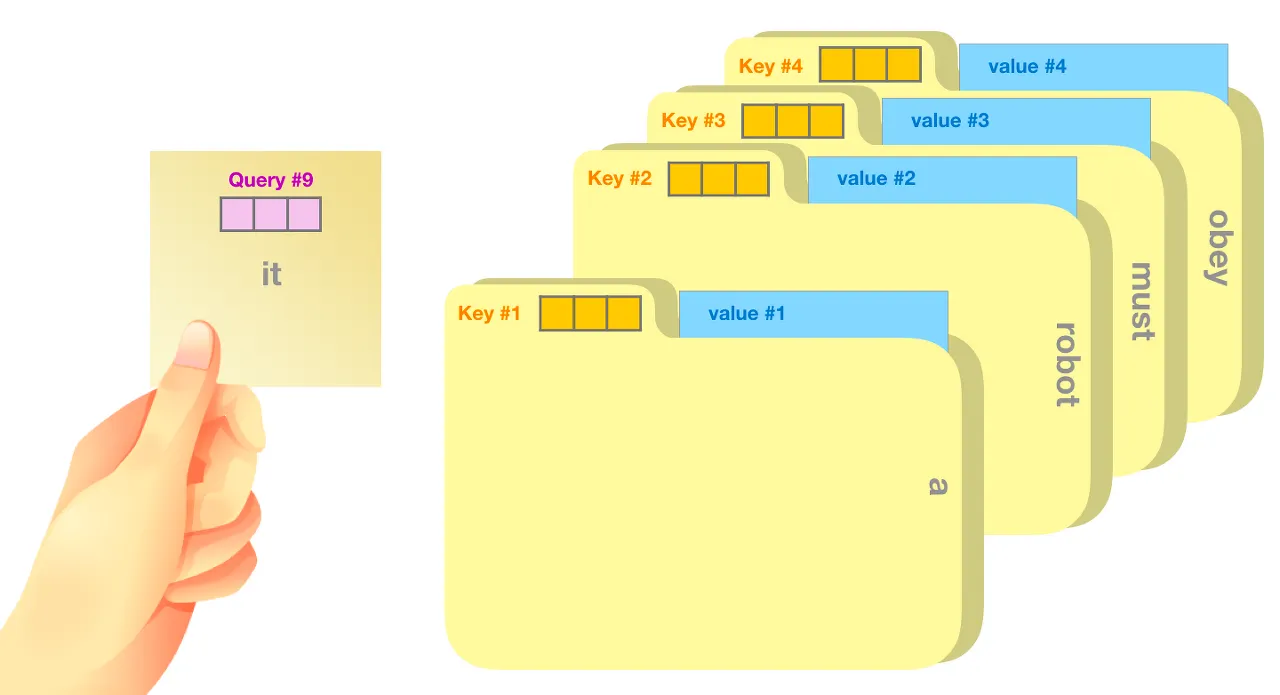
fi(x;{x1,...,xn})=σi(λx+γpool({x1,...,xn}))f_i(x;\{x_1, ..., x_n\}) = \sigma_i(\lambda x+ \gamma \text{pool}(\{x_1,...,x_n\}))
λ,γ:learnable scalar variables; σ(⋅):non-linear activation function\lambda, \gamma : \text{learnable scalar variables; } \sigma(\cdot): \text{non-linear activation function}

Attention

A set with nn elements = nn query vectors of dimension each dqd_q → Q∈Rn×dq:Query matrixQ \in \mathbb{R}^{n \times d_q}: \text{Query matrix}
An attention function Att(Q,K,V)\text{Att}(Q, K, V) maps queries QQ to outputs using nvn_v key-value pairs K∈Rnv×dq,V∈Rnv×dvK \in \mathbb{R}^{n_v \times d_q}, V \in \mathbb{R}^{n_v \times d_v}
Att(Q,K,V;ω)=ω(QK⊤)V\text{Att}(Q, K, V; \omega) = \omega(QK^\top)V
QK⊤:pairwise dot productQK^\top : \text{pairwise dot product} → measures how similar each pair of query and key vectors is.
ω:activation function\omega: \text{activation function}
usually, w(⋅)=softmax(⋅/d)w(\cdot) = \text{softmax}\Big(\cdot/\sqrt{d} \Big )
ω(QK⊤)V:weighted sum of V\omega(QK^\top)V: \text{weighted sum of } V
from huidea_tistory

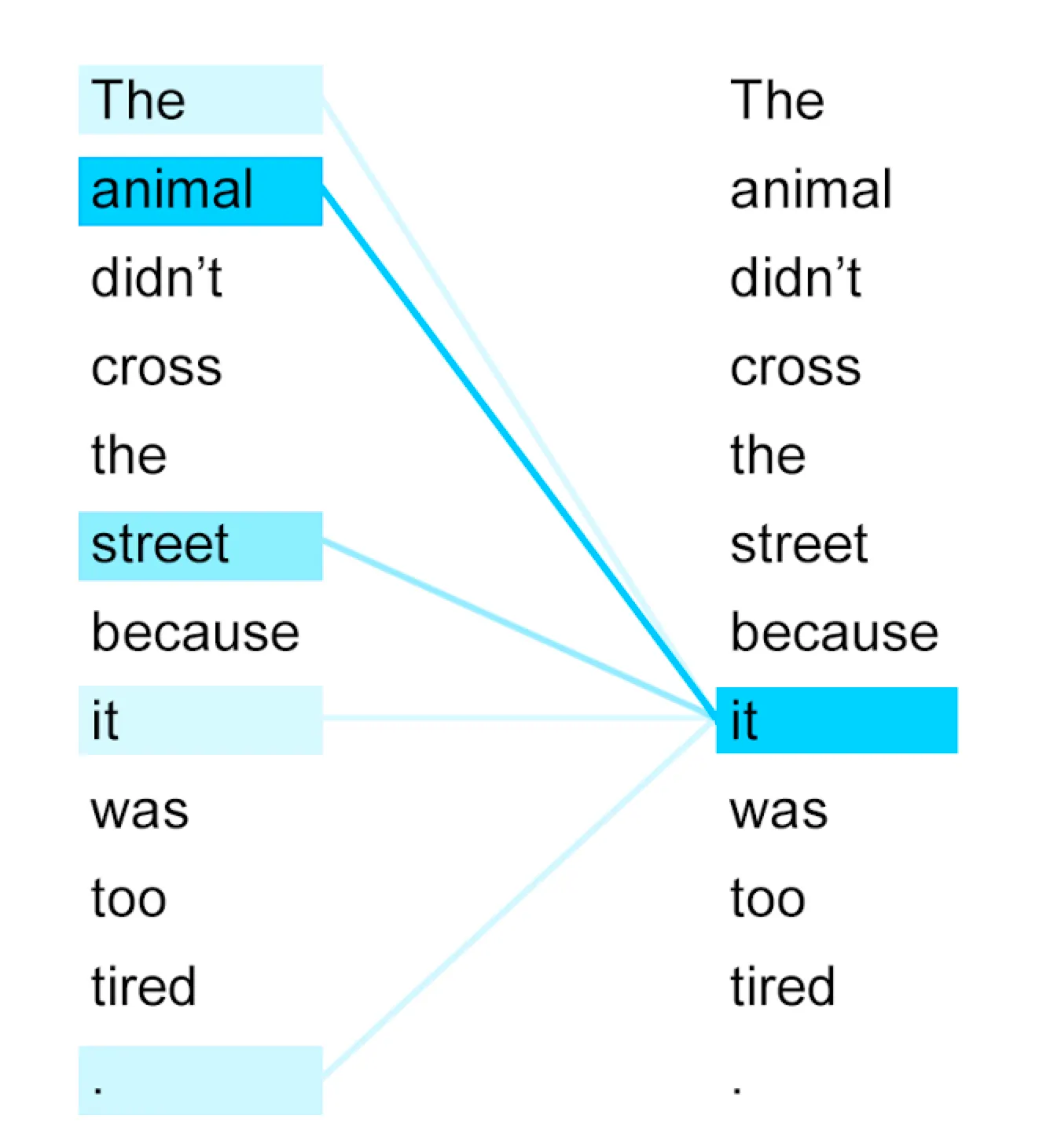
Self attention

From Google AI Blog
From Google AI Blog
•
Attention:
Attention score=⟨Hidden state of Encoder,Hidden state of Decoder⟩\text{Attention score} = \langle \text{Hidden state of Encoder},\text{Hidden state of Decoder} \rangle
•
Self-attention:
Attention score=⟨Hidden sate of Encoder, Hidden state of Encoder⟩\text{Attention score} = \lang \text{Hidden sate of Encoder, Hidden state of Encoder} \rang
→ Can approximate interactions between input data

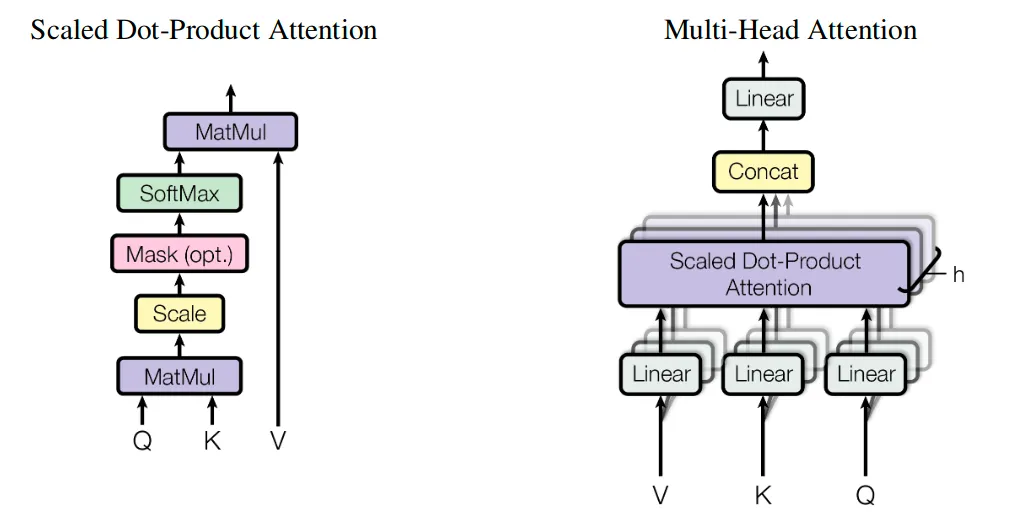
Multi-head self-attention

Instead of computing a single attention function, this method first projects Q,K,VQ, K, V onto hh different dqM,dqM,dvMd^M_q, d^M_q, d^M_v-dimensional vectors
Multihead(Q,K,V;λ,ω)=concat(O1,...,Oh)WO\text{Multihead}(Q, K, V; \lambda, \omega) = \text{concat}(O_1, ...,O_h) W^O
where Oj=Att(QWjQ,KWjK,VWjV;ω)\text{where } O_j = \text{Att}(QW^Q_j, KW^K_j, VW^V_j ;\omega)
From Attention is all you need

4. Deep-dive

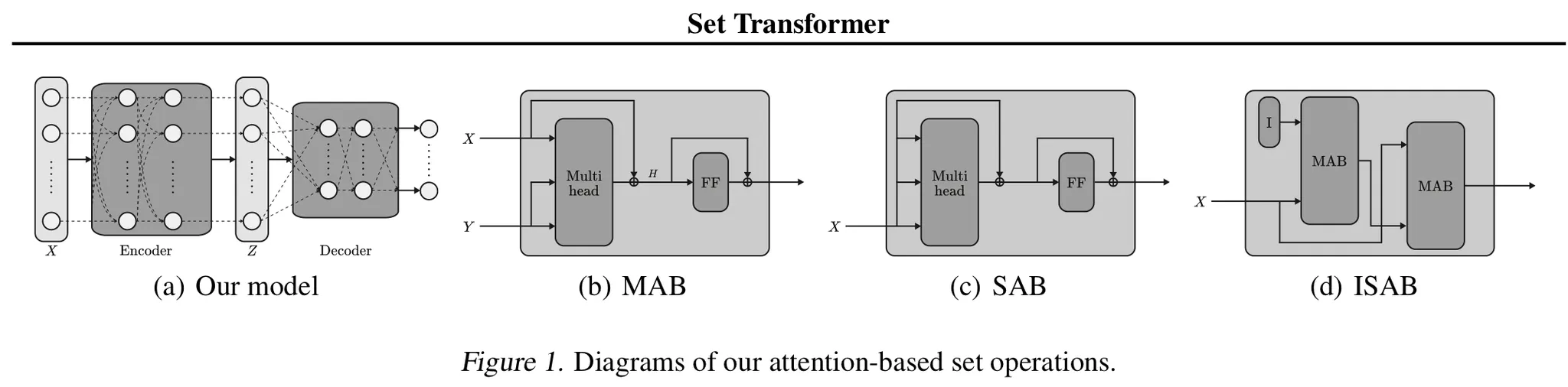
4.1. Permutation equivariant (induced) set attention blocks

4.1.1. Taxonomies

MAB:Multihead Attention Block\text{MAB}: \text{Multihead Attention Block}
SAB:Set Attention Block\text{SAB}: \text{Set Attention Block}
ISAB:Induced Set Attention Block\text{ISAB} : \text{Induced Set Attention Block}
X,Y∈Rn×d:sets of d-dimensional vectorsX, Y \in \mathbb{R}^{n \times d}: \text{sets of } d \text{-dimensional vectors} → Matrix
rFF:any row-wise feedforward layer\text{rFF}: \text{any row-wise feedforward layer} → processes each instance independently and identically

4.1.2. MAB

MAB(X,Y)=LayerNorm(H+rFF(H))\text{MAB}(X, Y) = \text{LayerNorm}(H+\text{rFF}(H))
where H=LayerNorm(X+Multihead(X,Y,Y;ω))\text{where }H = \text{LayerNorm}(X + \text{Multihead}(X, Y, Y; \omega))
c.f.) MAB\text{MAB} is an encoder block of the Transformer without positional encoding and dropout

4.1.3. SAB

A special form of MAB
SAB(X)=MAB(X,X)\text{SAB}(X) = \text{MAB}(X, X)
→ SAB\text{SAB} takes a set and performs self-attention.
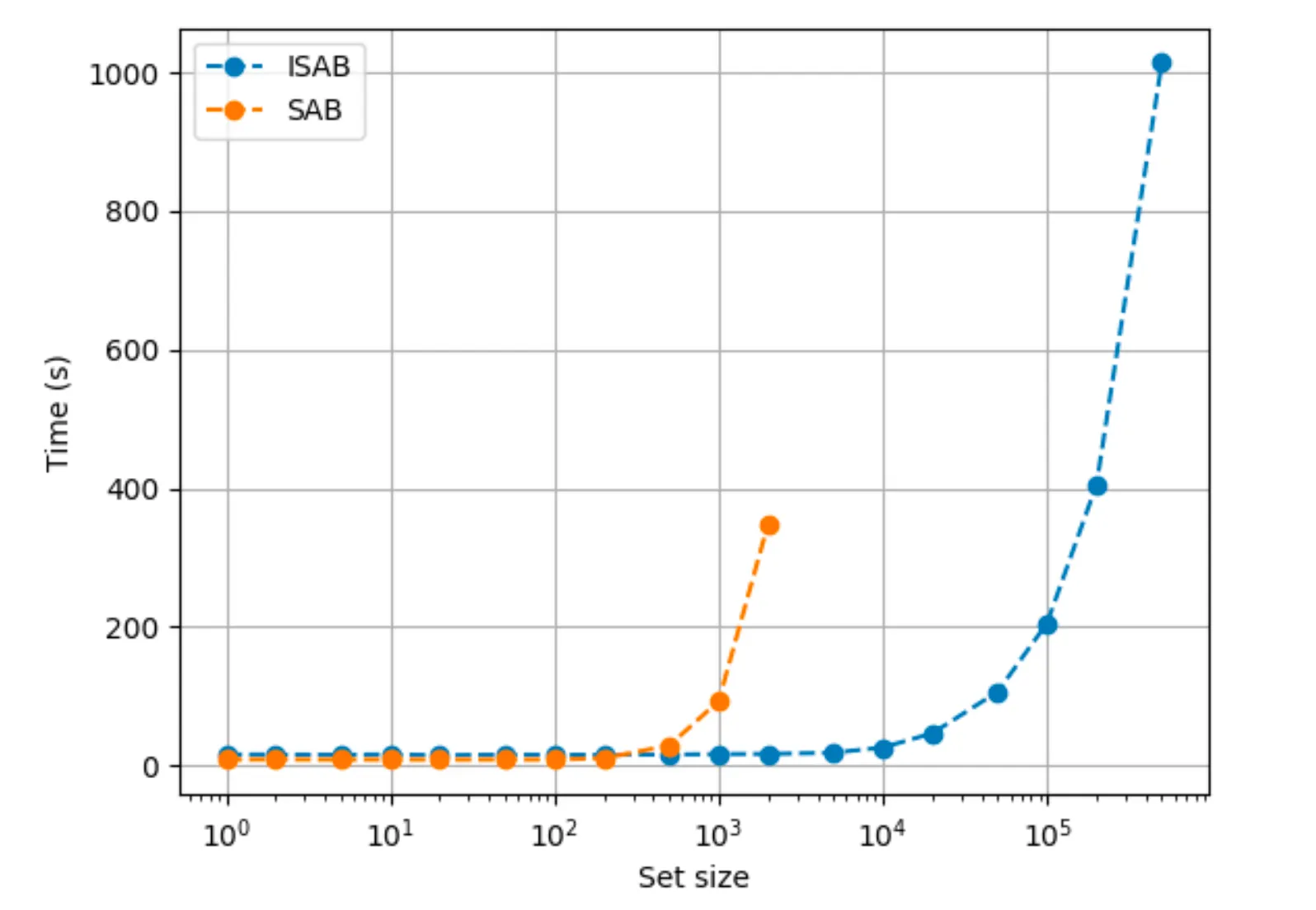
But, a potential problem of using SABs is the quadratic time complexity O(n2)\mathcal{O}(n^2)
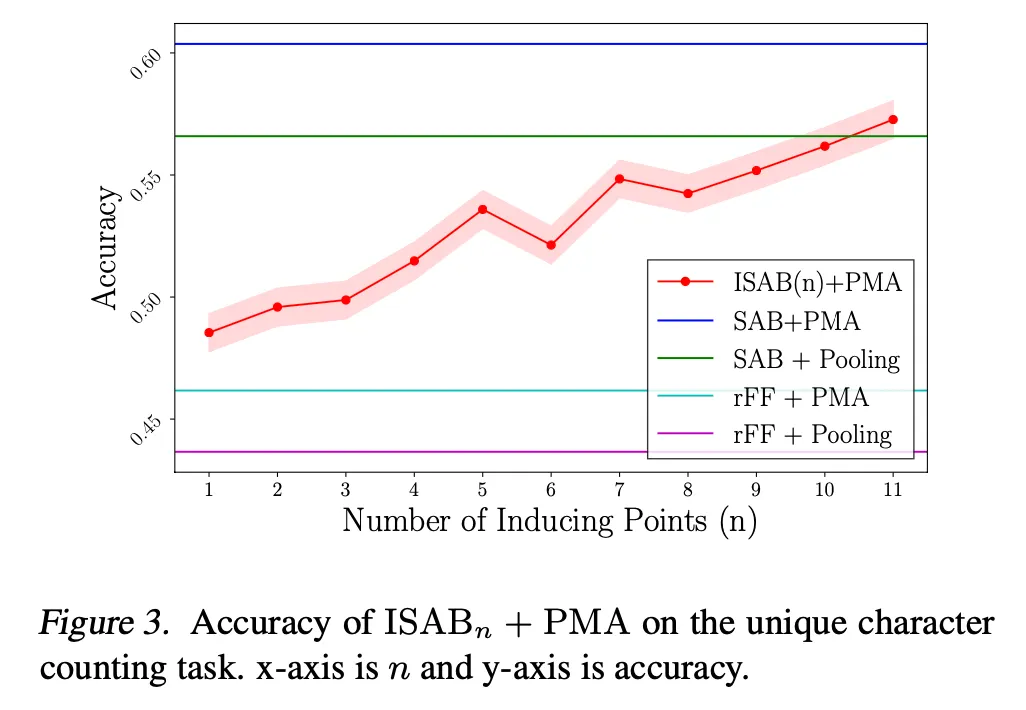
→ Authors introduce the ISAB(Induced Set Attention Block)

4.1.4. ISAB

Additionally define mm dd-dimensional vectors I∈Rm×d:inducing pointsI \in \mathbb{R}^{m \times d}: \text{inducing points} ← trainable parameters
ISABm(X)=MAB(X,C)∈Rn×d\text{ISAB}_m(X) = \text{MAB}(X, C) \in \mathbb{R}^{n \times d}
where C=MAB(I,X)∈Rm×d\text{where } C= \text{MAB}(I, X) \in \mathbb{R}^{m \times d}
1.
Transform II into CC by attending to the input set.
2.
CC : the set of transformed inducing points, which contains information about XX, is again attended to by XX to finally produce a set of nn elements.
→ Similar to low-rank projection or autoencoder, but the goal of ISAB is to obtain good features for the final task.
e.g.) In amortized clustering, the inducing points could be the representation of each cluster.
Time complexity of ISAB is O(nm)\mathcal{O}(nm) → Linear!
m:hyperparameterm: \text{hyperparameter}
Both SAB(X),ISABm(X) are permutation equivariant!\text{Both }\text{SAB}(X), \text{ISAB}_m(X) \text{ are permutation equivariant!}

4.2. Pooling by Multi-head attention

Common aggregation scheme: dimension-wise average or maximum
Instead, authors propose applying multi-head attention on a learnable set of kk seed vectors S∈Rk×dS \in \mathbb{R}^{k \times d}. Z∈Rn×dZ \in \mathbb{R}^{n \times d} is the set of features constructed from an encoder.
PMA:Pooling by Multihead attention\text{PMA}: \text{Pooling by Multihead attention} with kk seed vectors
PMAk(Z)=MAB(S,rFF(Z))\text{PMA}_k(Z) = \text{MAB}(S, \text{rFF}(Z))
Output of PMAk\text{PMA}_k is a set of kk items.
In most cases, k=1k = 1
But for tasks such as amortized clustering which requires kk correlated outputs, we need to use kk seed vectors
To further model the interactions among the kk outputs, authors apply SAB
T=SAB(PMAk(Z))T = \text{SAB}(\text{PMA}_k(Z))

4.3. Overall Architecture

Need to stack multiple SABs to encode higher order interactions.
Encoder:X↦Z∈Rn×d\text{Encoder}: X \mapsto Z \in \mathbb{R}^{n \times d}
Encoder(X)=SAB(SAB(X))\text{Encoder}(X) = \text{SAB}(\text{SAB}(X))
Encoder(X)=ISABm(ISABm(X))\text{Encoder}(X) = \text{ISAB}_m(\text{ISAB}_m(X))
Time complexity for l\mathcal{l} stacks of SABs and ISABs are O(ln2)\mathcal{O}(ln^2) and O(lnm)\mathcal{O}(lnm)
Decoder aggregates ZZ into a single or a set of vectors which is fed into a feed-forward network to get final outputs.
Decoder(Z;λ)=rFF(SAB(PMAk(Z)))∈Rk×d\text{Decoder}(Z; \lambda) = \text{rFF}(\text{SAB}(\text{PMA}_k(Z))) \in \mathbb{R}^{k \times d}

4.4. Analysis

The encoder of the set transformer is permutation equivariant.
But the set transformer is permutation invariant.

5. Experiments

5.1. Toy problem: Maximum value regression

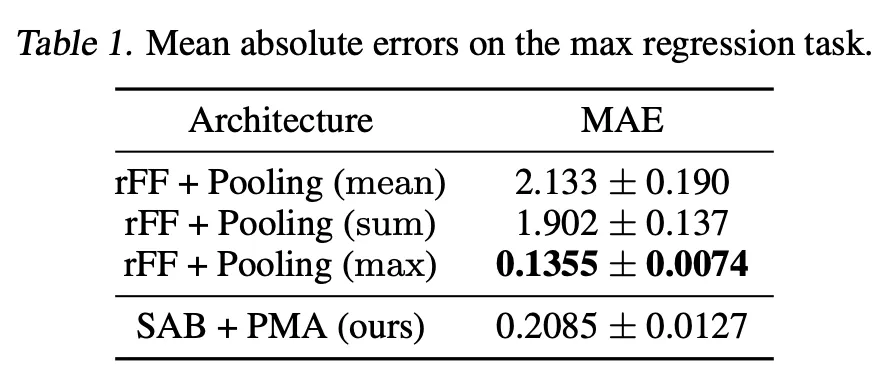
Motivation: Can the model learn to find and attend to the maximum element?
The model with max-pooling can predict the output perfectly by learning its encoder to be an identity function.
Set transformer achieves comparable performance to the max-pooling model.

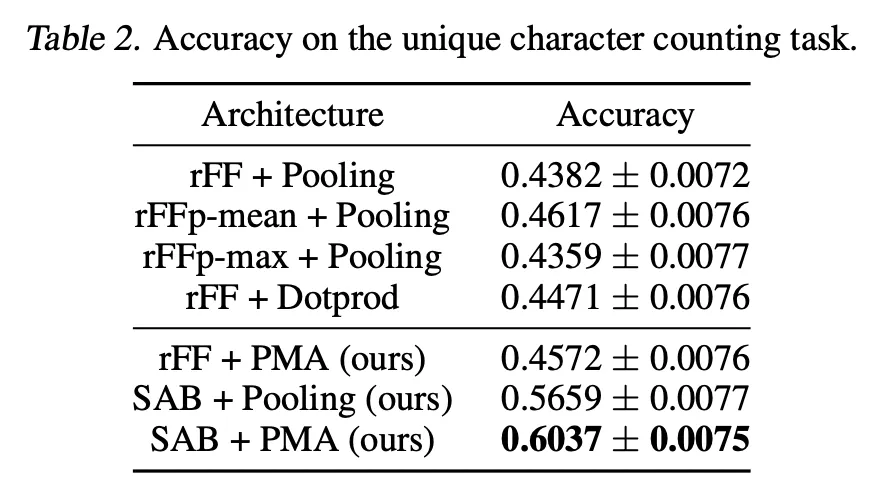
5.2. Counting unique characters

Motivation: Can the model learn the interactions between objects in a set?
Dataset: Omniglot
Goal: Predict the number of different characters inside the set

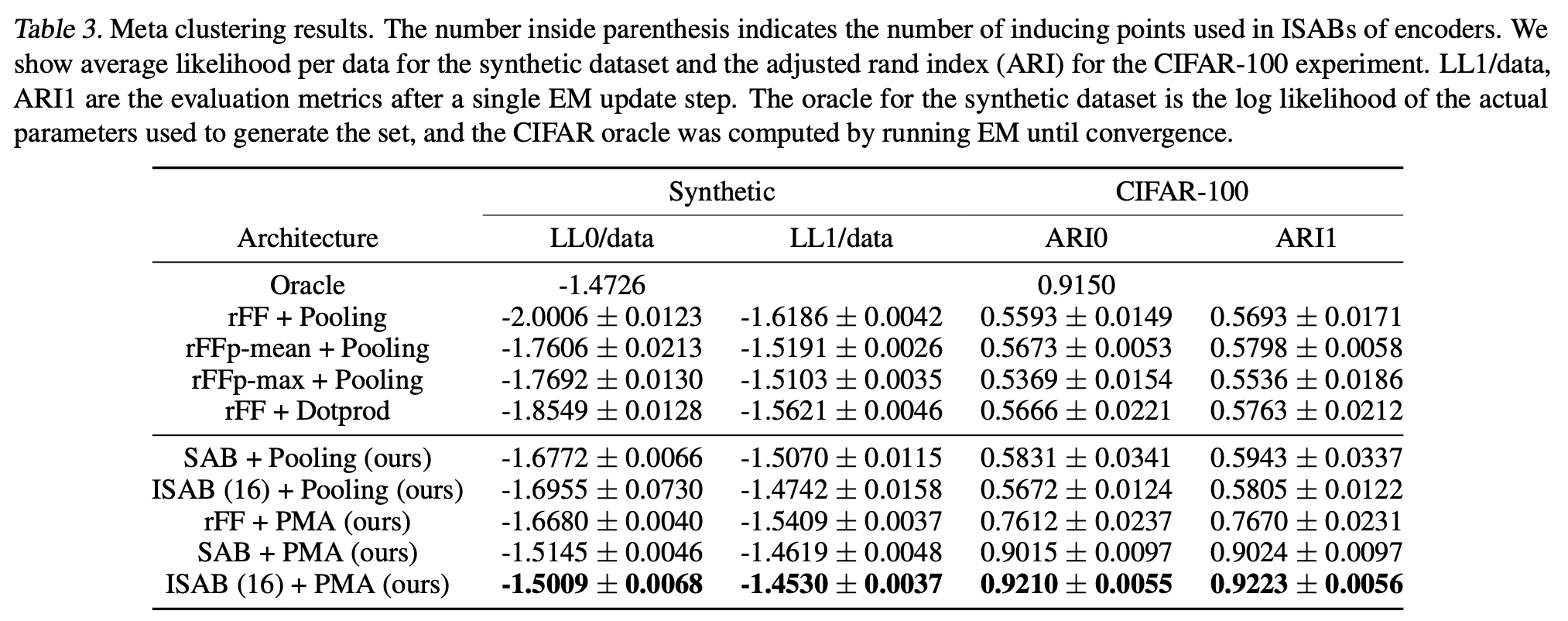
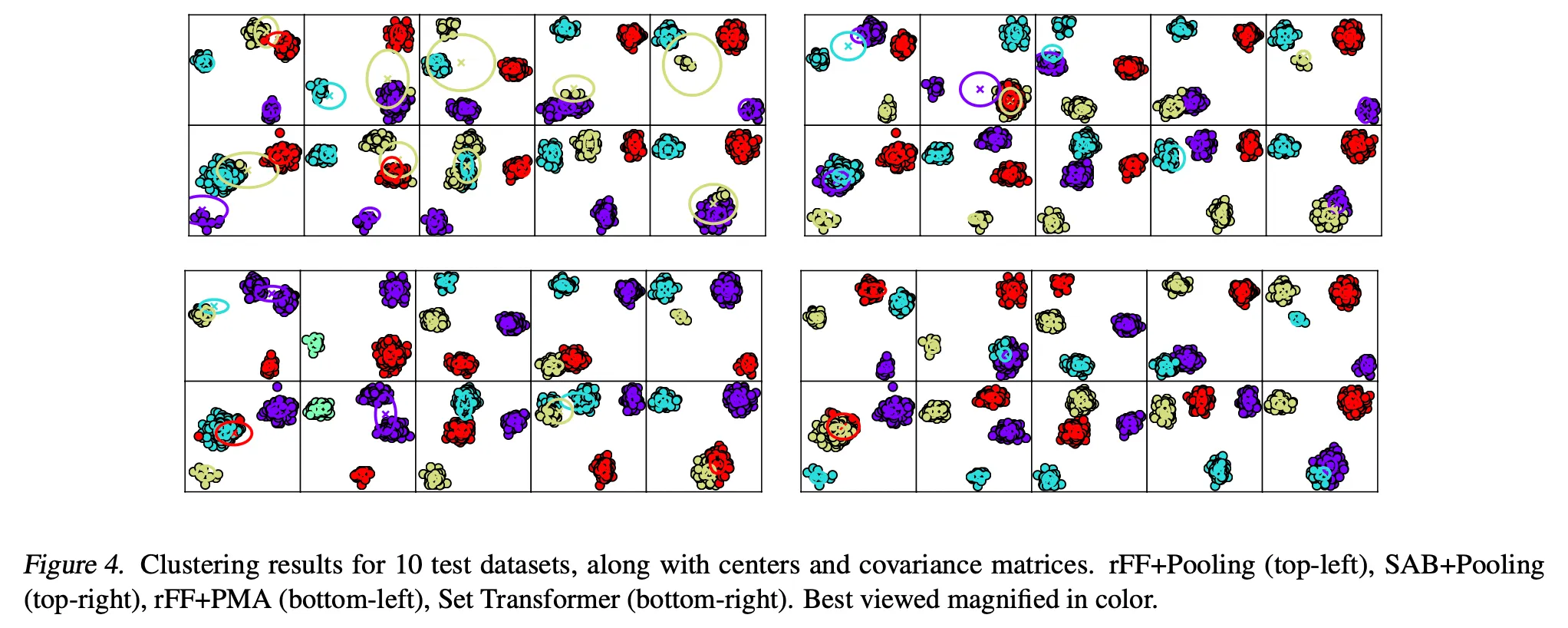
5.3. Amortized clustering with mixture of Gaussians

The log-likelihood of a dataset X={x1,...,xn}X = \{ x_1, ..., x_n\}
log⁡p(X;θ)=∑i=1nlog⁡∑j=1kπjN(xi;μj,diag(σj2))\log p(X; \theta) = \sum^n_{i=1} \log \sum^k_{j=1} \pi_j \mathcal{N}(x_i;\mu_j, \text{diag}(\sigma^2_j))
Typical approach is to run an EM algorithm until convergence.
Dataset:
•
Synthetic 2D mixtures of Gaussians
•
Vectors from pretrained VGG network trained on CIFAR-100
Goal: Learn a generic meta-algorithm that directly maps the input set XX to θ∗(X)\theta^*(X)

6. Conclusion

Why I chose this article
From Meta Learning in Neural Networks: A Survey
From Set Transformer