Summary
•
Authors propose Low-Rank Adaptation (LoRA) that freezes the pretrained model weights and injects trainable rank decomposition matrices.
•
LoRA reduced the number of trainable parameters and improved efficiency without no critical drop in accuracy and no additional inference latency.
◦
GPT-3 175B: 1/10,000 times # of parameters, 1/3 GPU memory
•
LoRA is task- and model-agnostic. (Can be applied to many fine-tuning regime)
Related works
(Typical) Adapter layers
•
Most of the adapter layers introduce inference latency.
◦
Houlsby et al. (2019) - two adapter layers
◦
Lin et al. (2020)
•
Since the batch size of most online inference is 1, this induces noticeable increase in inference time.
Low-rank structures in Deep Learning
•
Low-rank structure:
◦
The property that the tensors of the neural network (usually weight matrices) can be approximated or decomposed into a combination of low-rank matrices or tensors.
◦
Have been observed in various deep learning tasks (especially in over-parametrized neural networks)
Fine-tuning
•
Full fine-tuning:
◦
The model is initialized to pre-trained weights .
◦
And updated to
◦
Extremely compute-intensive for large models (such as GPT-3 with 175 Billion parameters)
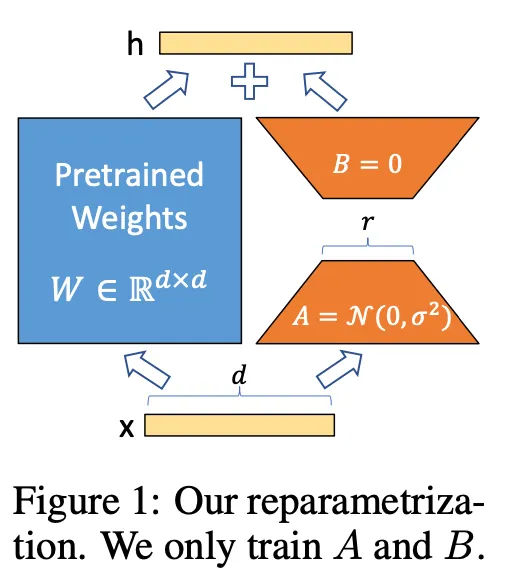
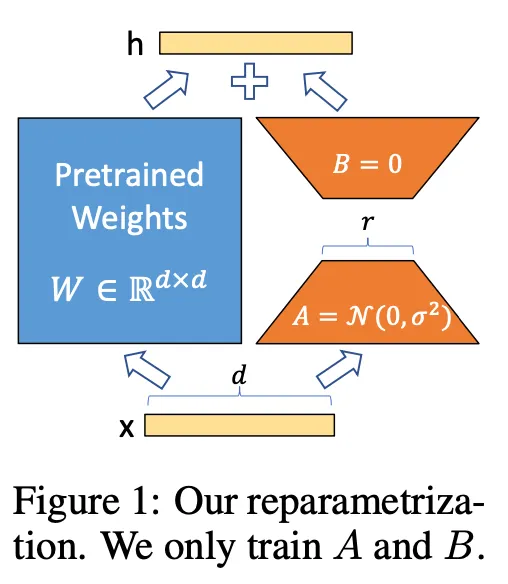
LoRA
•
Low-rank Adaptation
◦
Task-specific parameter increment is encoded by much smaller sized set of parameters . → Compute- and memory-efficient!
•
Applying to Transformer
◦
LoRA is applied to only self-attention module weights -
▪
Not applied to MLP module
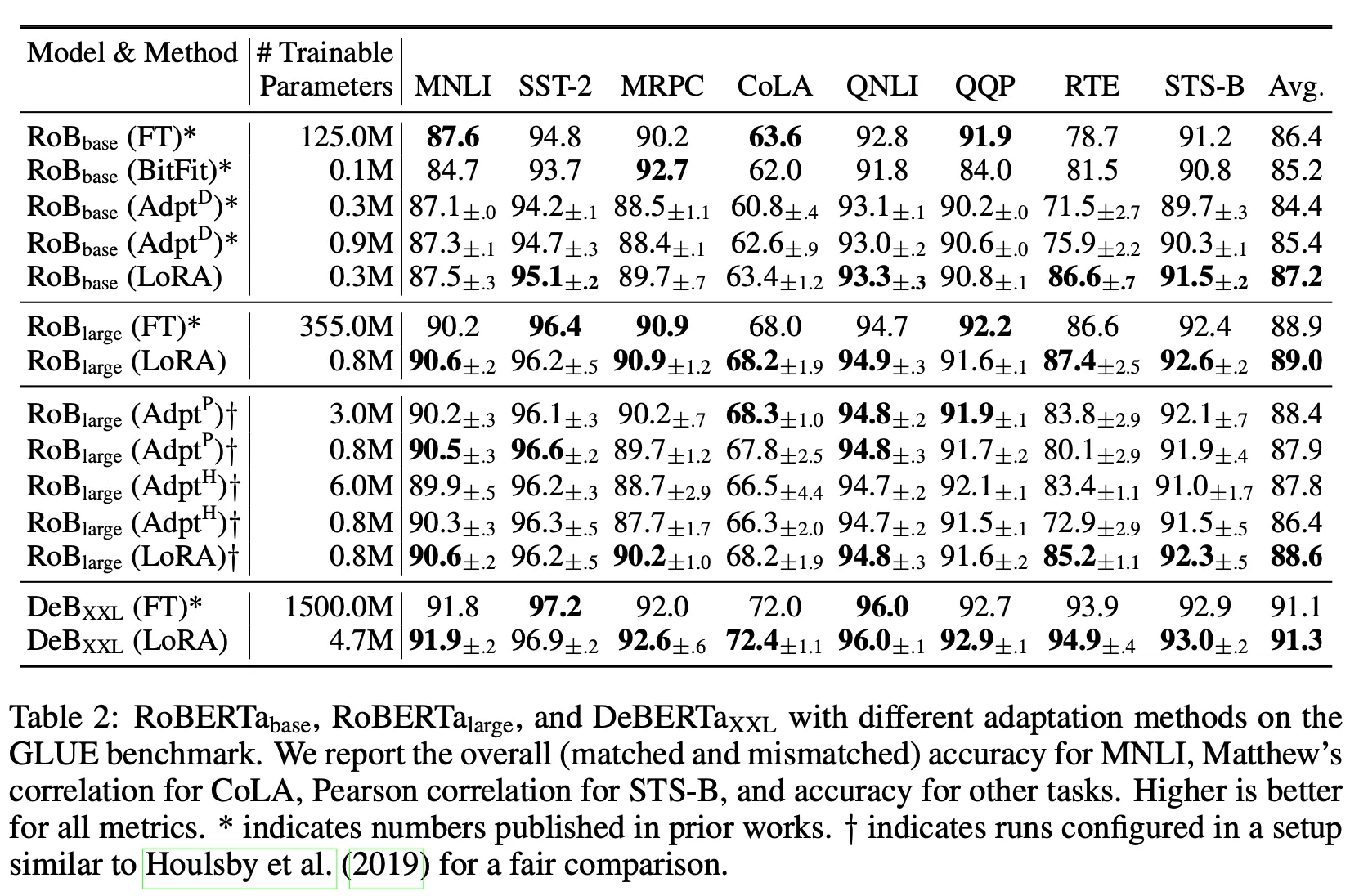
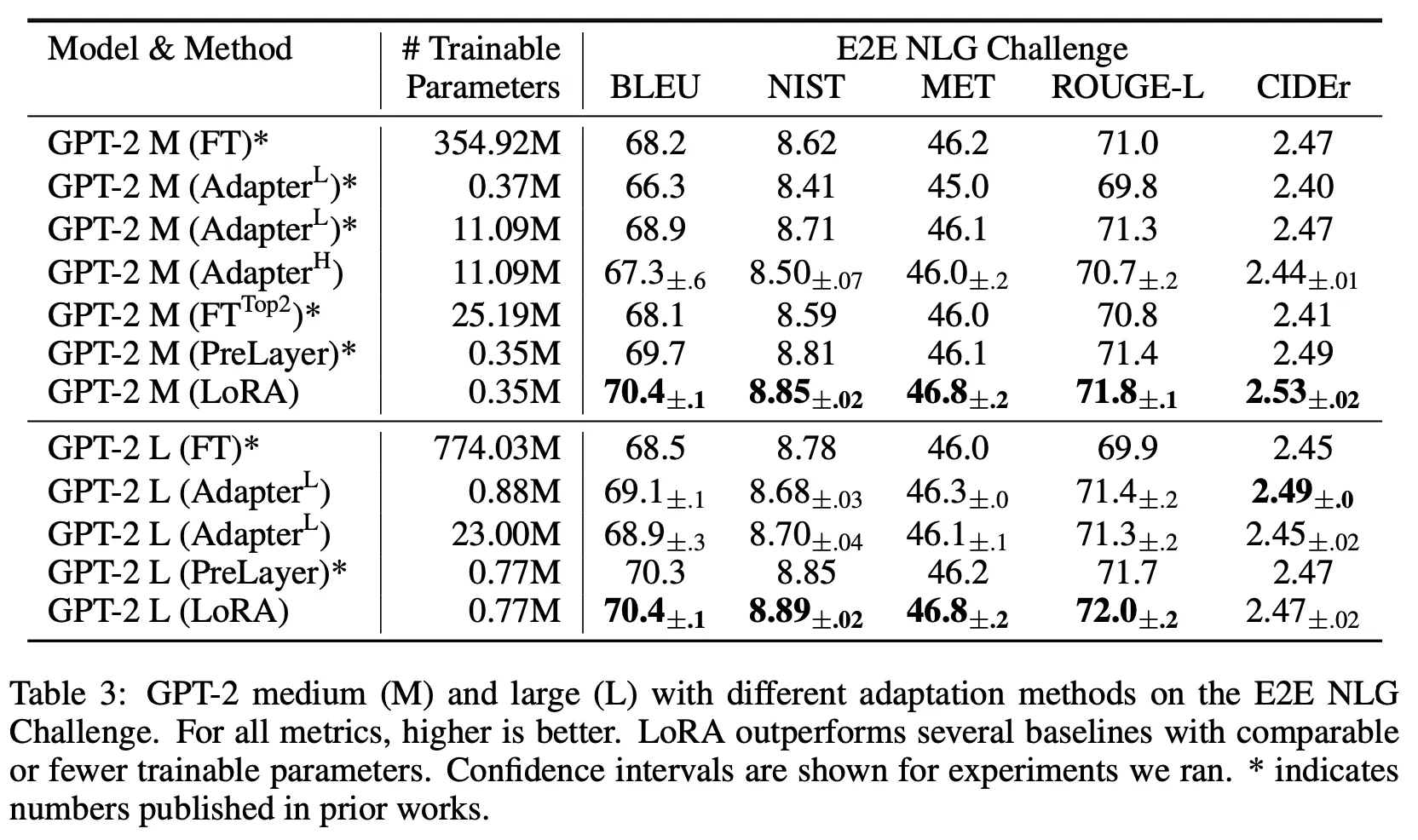
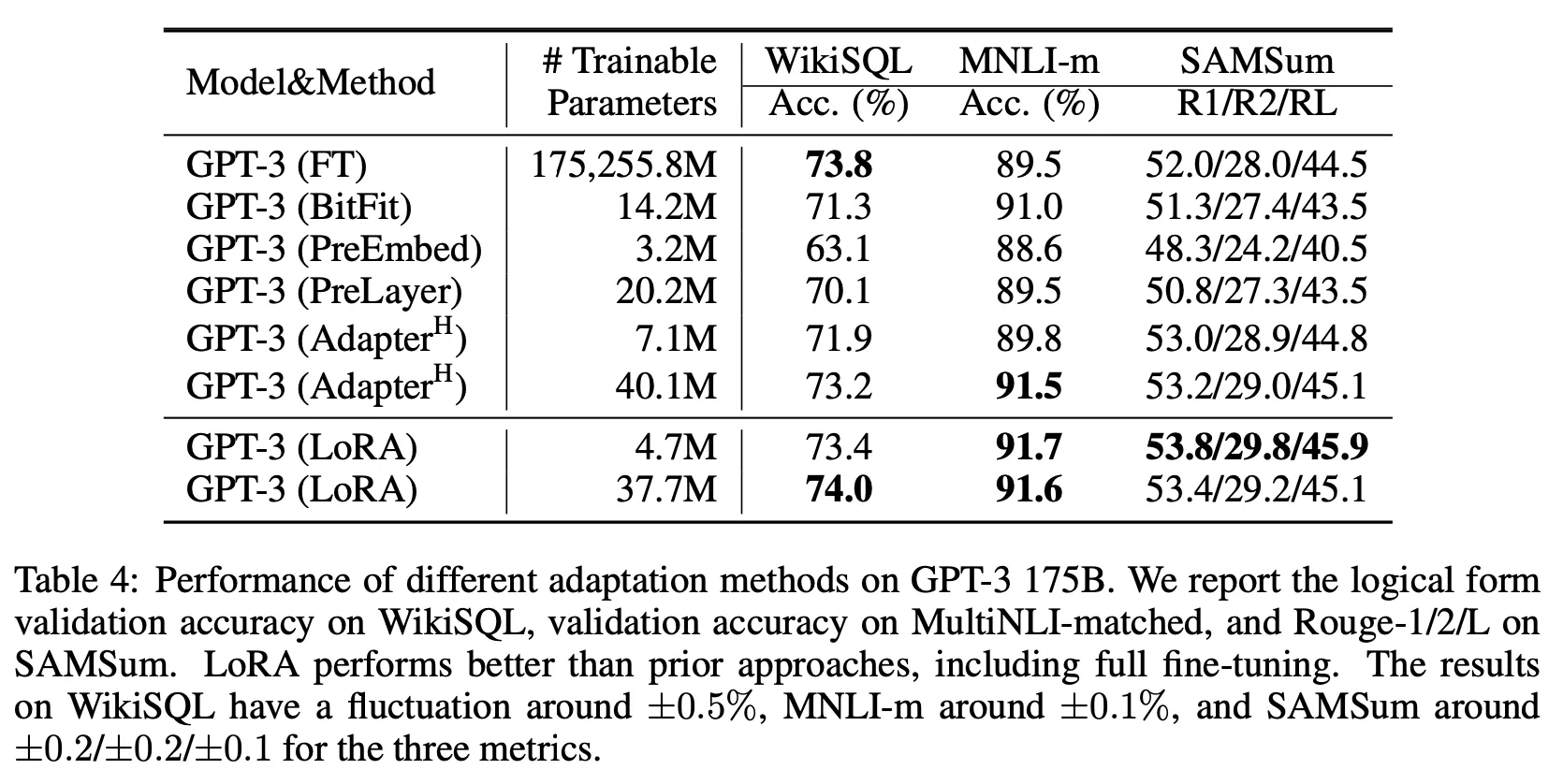
Results
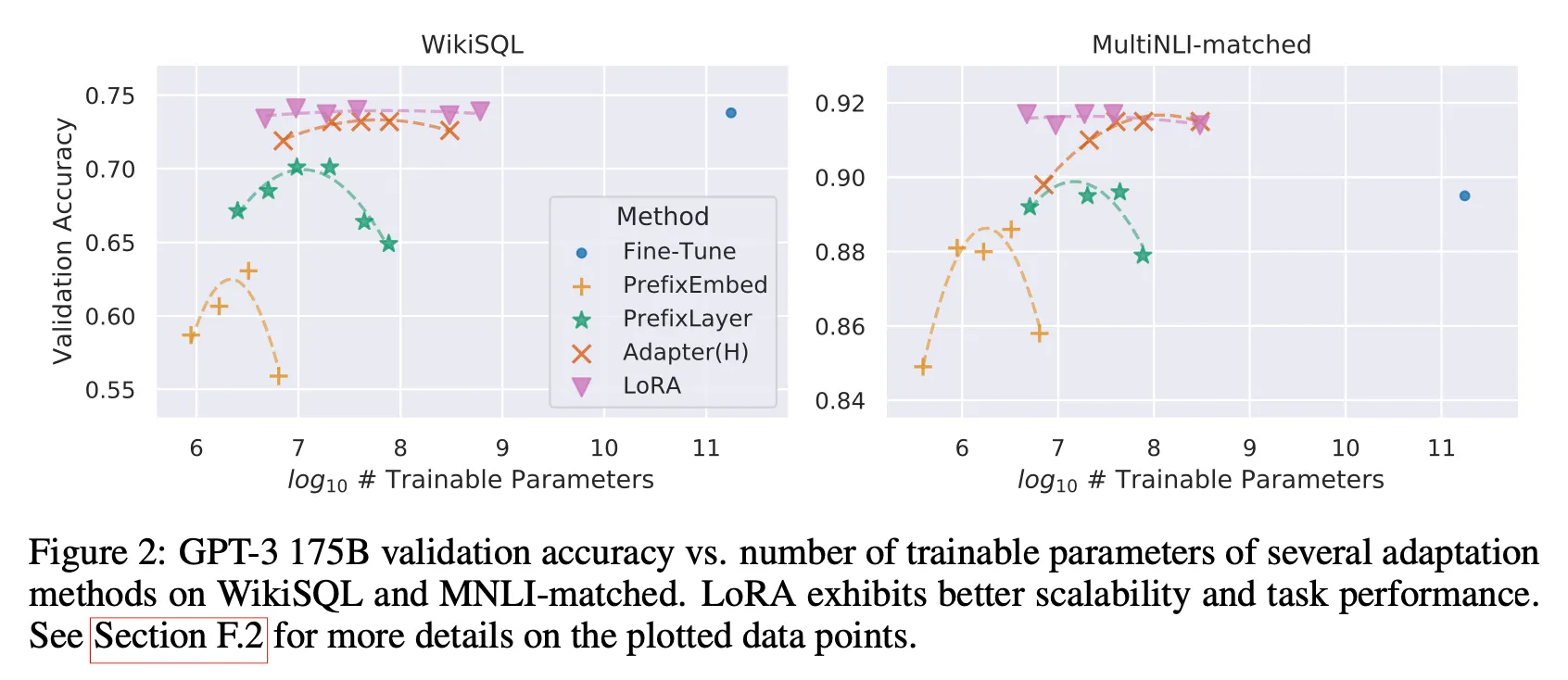
Further analysis
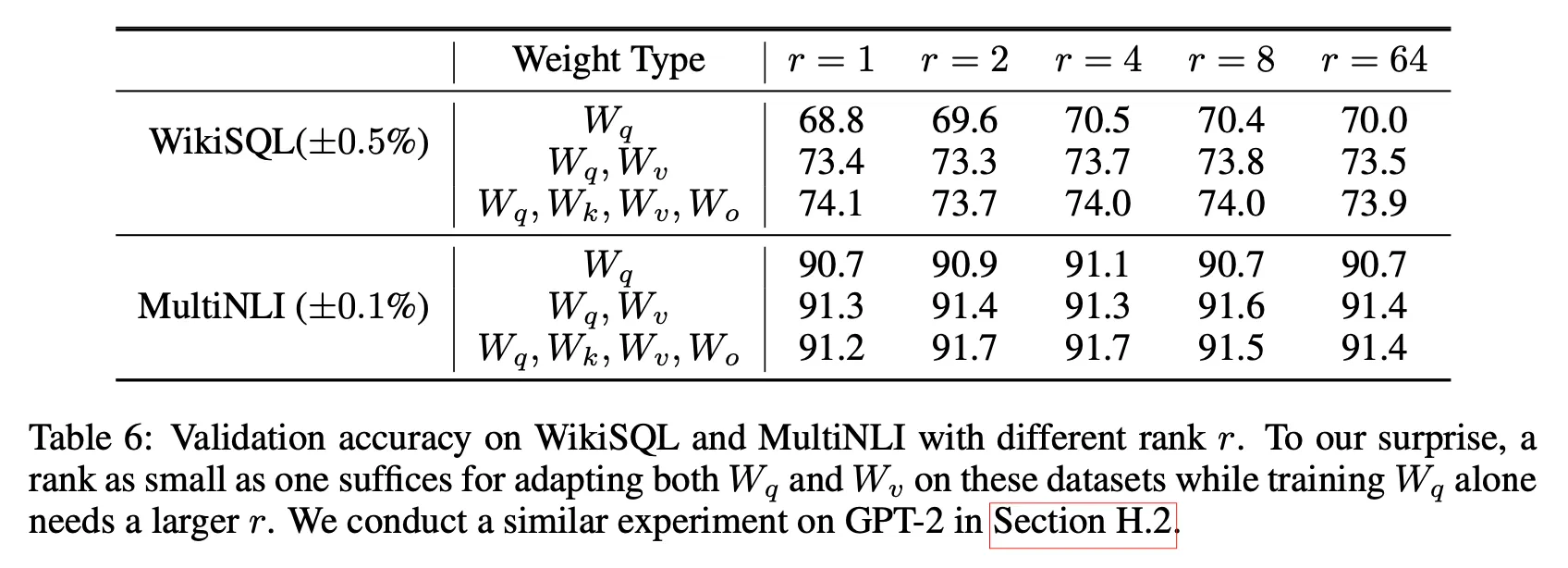
Optimal rank for LoRA?
•
LoRA performs well even with a very small
•
Increasing does not cover a more meaningful subspace
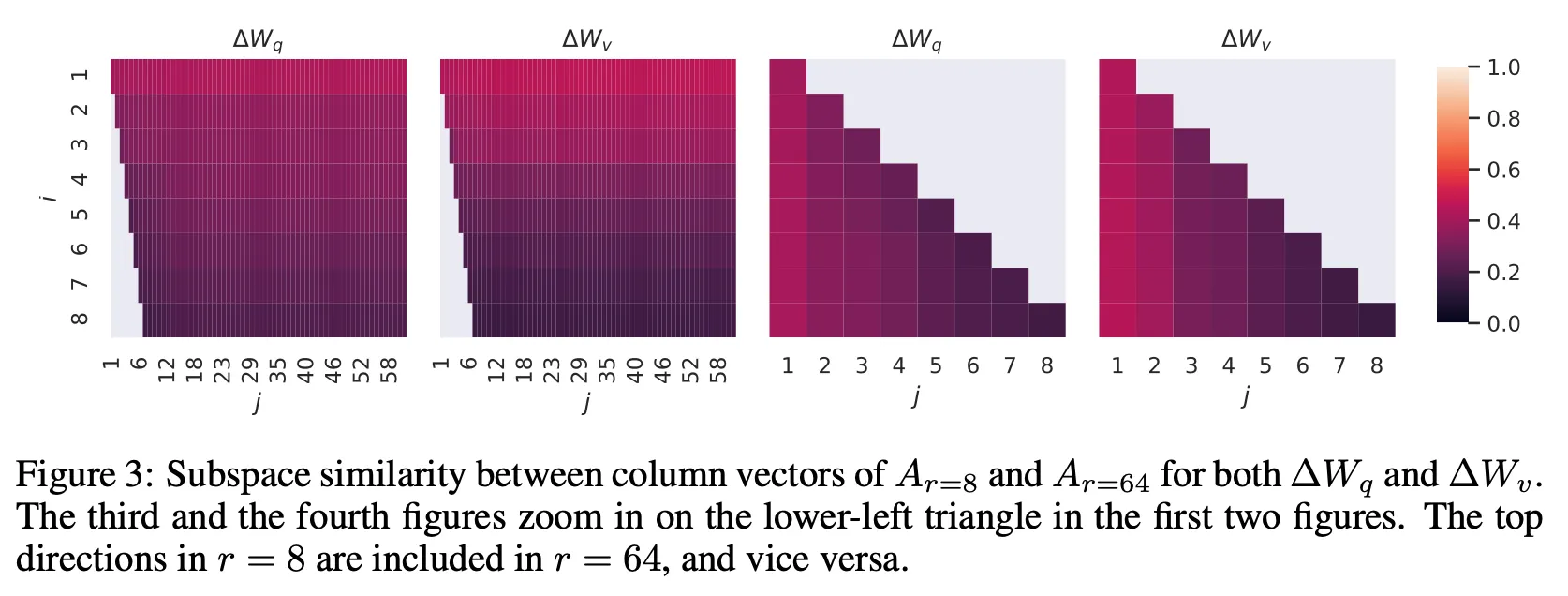
Subspace similarity between different
•
Directions of top singular vector overlaps significantly, while others are not.