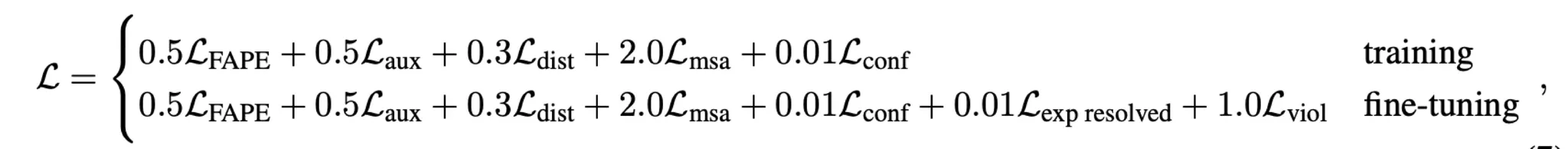Search

AlphaFold2 Explained

Introduction

If you need some background information about protein folding, refer to Introduction to Protein Folding

From AlphaGo to AlphaFold, from games to science

I recommend reading the above interview of Demis Hassabis as a good introduction about AlphaFold.

AlphaFold2 (AF2)

The end-to-end foundation deep learning model for protein structure prediction

Keywords and novelties of AF2

1.
End-to-end
2.
Evoformer
3.
Backbone frame, torsion angle
4.
Invariant point attention (IPA)
5.
FAPE loss
6.
Self-distillation
7.
Self-estimates of accuracy (confidence metrics)

Background

Some backgrounds to understand AF2. You can always come back here
Multiple sequence alignment (MSA)
Residues and side chains
Distogram
Rigid body assumption

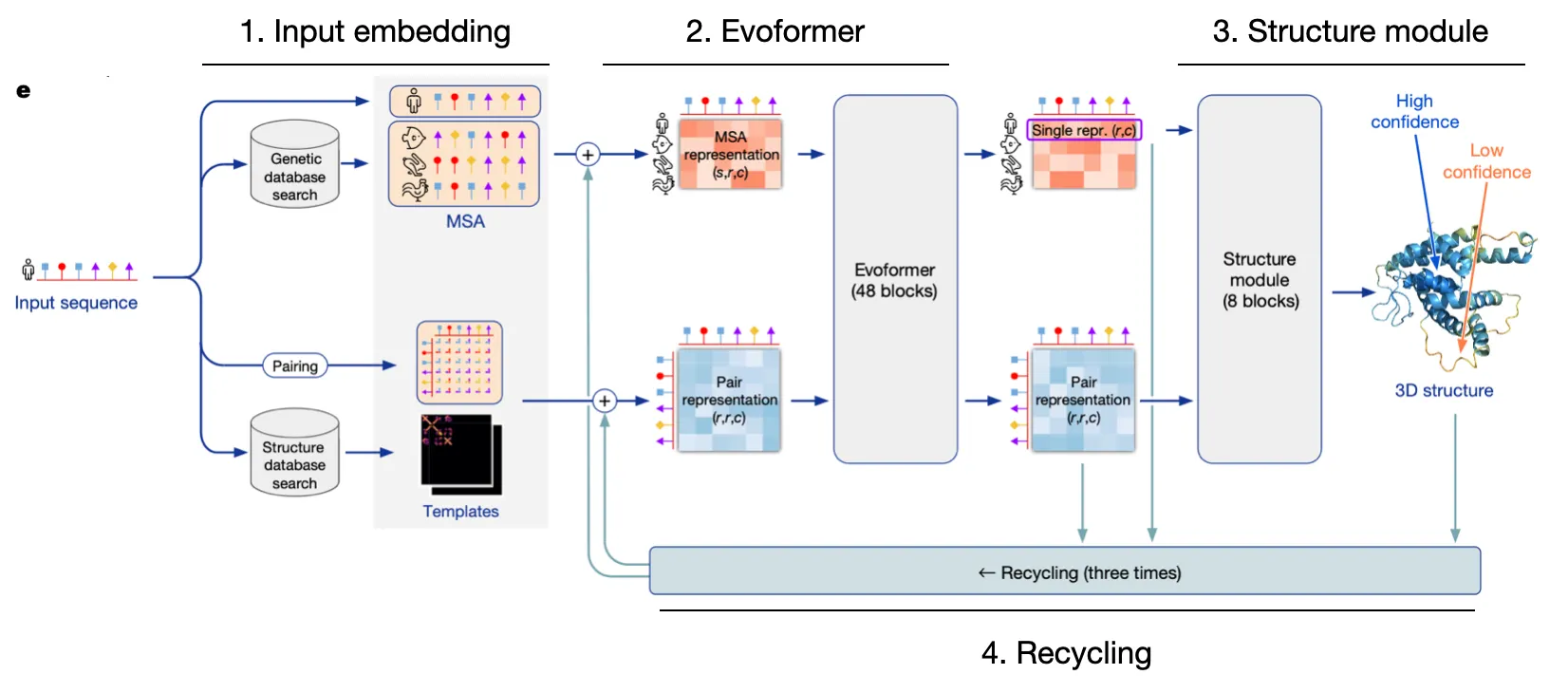
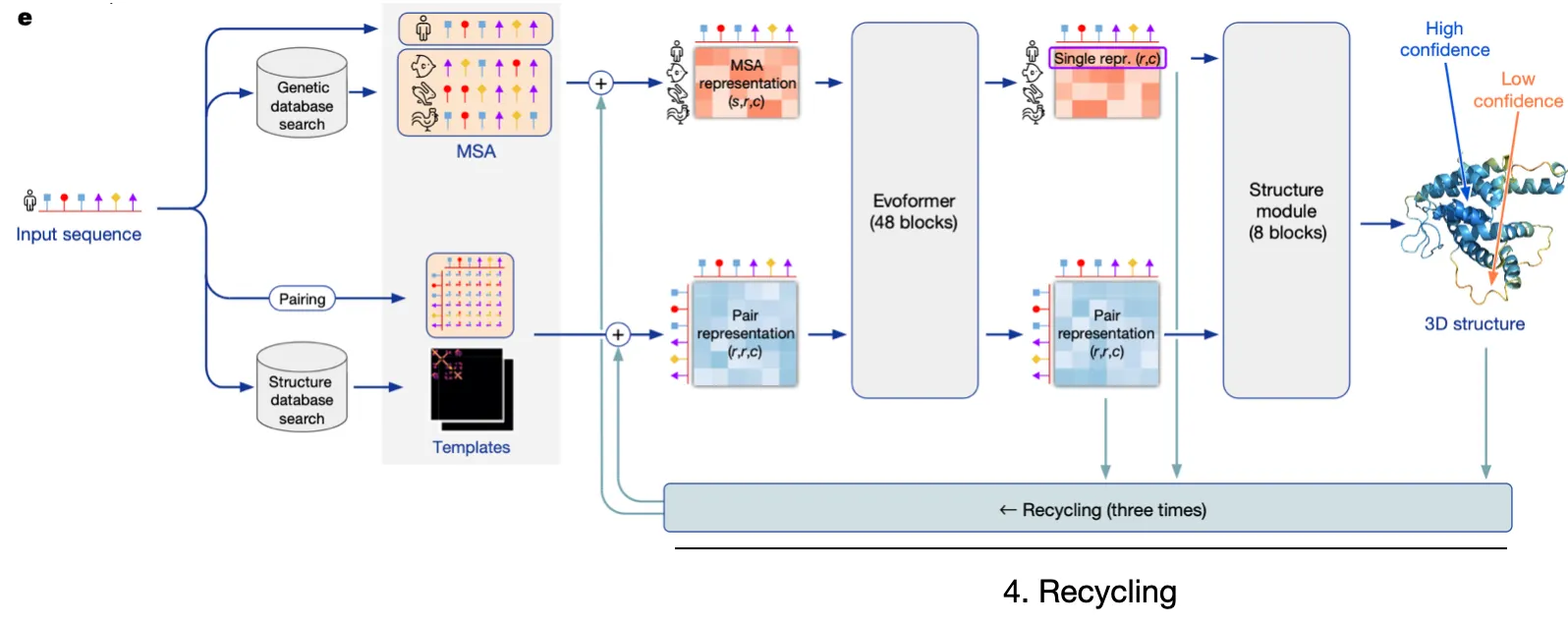
AF2 Model I/O and Overview

AF2 is extremely intricate, but let's simplify it into four pillars
1.
Input embedding
Embed relevant sequence information and structural details into embedding vectors.
2.
Evoformer
Utilize efficient & robust self-attention to update MSA rep & Pair rep, while exchanging information between the two.
3.
Structure module
Explicitly predict structure with Invariant Point Attention
4.
Recycling
Refine predictions through recycling

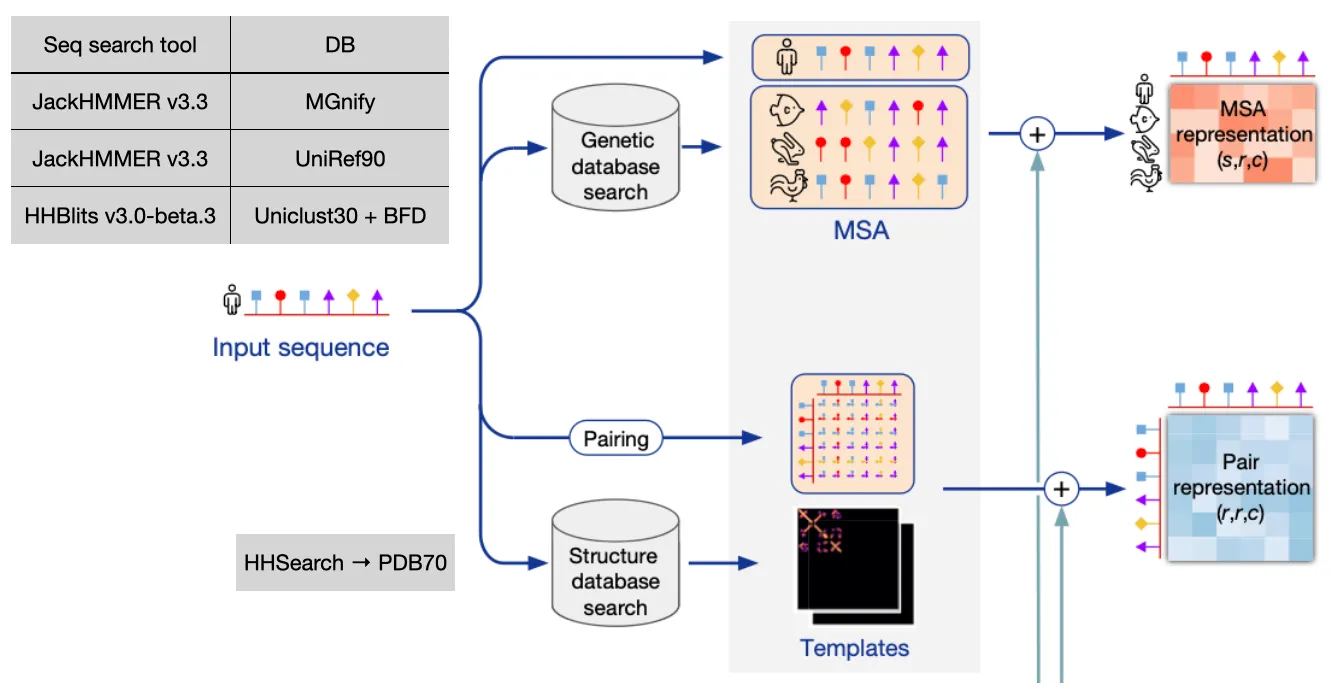
Input embedding

Input: Amino acid sequence Output: MSA representation (NseqΓ—NresΓ—cm)(N_{seq}\times N_{res} \times c_m) & Pair representation (NresΓ—NresΓ—cz)(N_{res} \times N_{res} \times c_z) Goal: Find similar sequences from database and build initial feature of the input sequence using that information
1.
Sequence info
Finds similar sequences from the database, and align them with MSA algorithms.
Why do we need MSA information to predict protein structure?
Answer: Because MSA can capture homology and evolutionary relationships between the query sequence and related sequences.
more..
MSA matrix carries sequential evolutionary covariation information!
β€’
Genetic search (MSA)
Find evolutionary context of input sequence, perform profile HMM-based DB search
2.
Structure info
Finds already known similar structure template information, which can give explicit hints to the model!
β€’
Template search
With the MSA result (especially JackHMMER v3.3 + UniRef90), use HHSearch on PDB70 to find similar structures
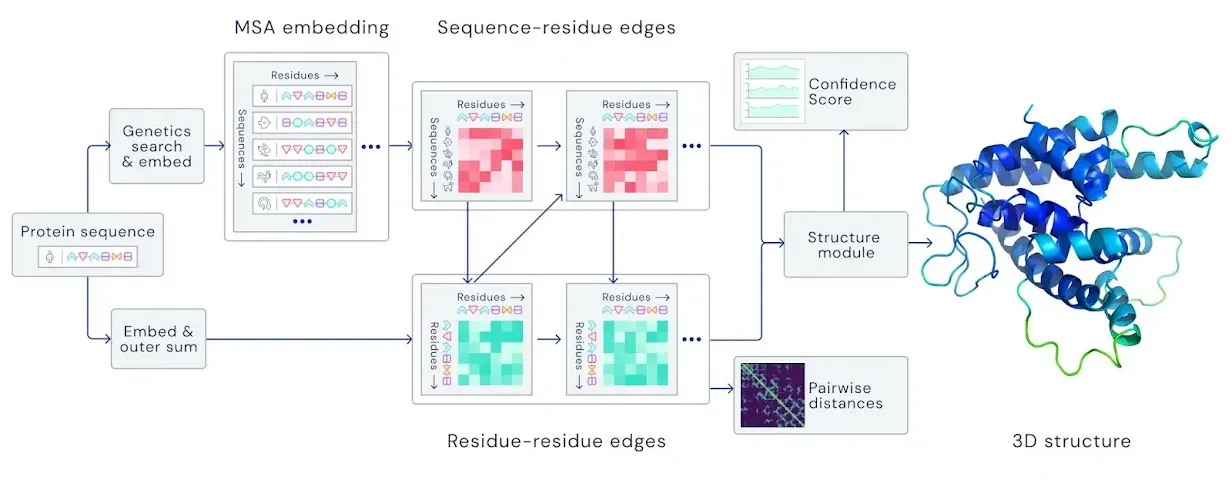
Both sequence info and structure info is used to build MSA representation and Pair representation. Detailed workflow Β (take a good look at their dimensions!)
Input feature embedding at a glance
Spoiler!
The first row of MSA representation is from the query sequence. This row is later called as β€˜Single representation’.

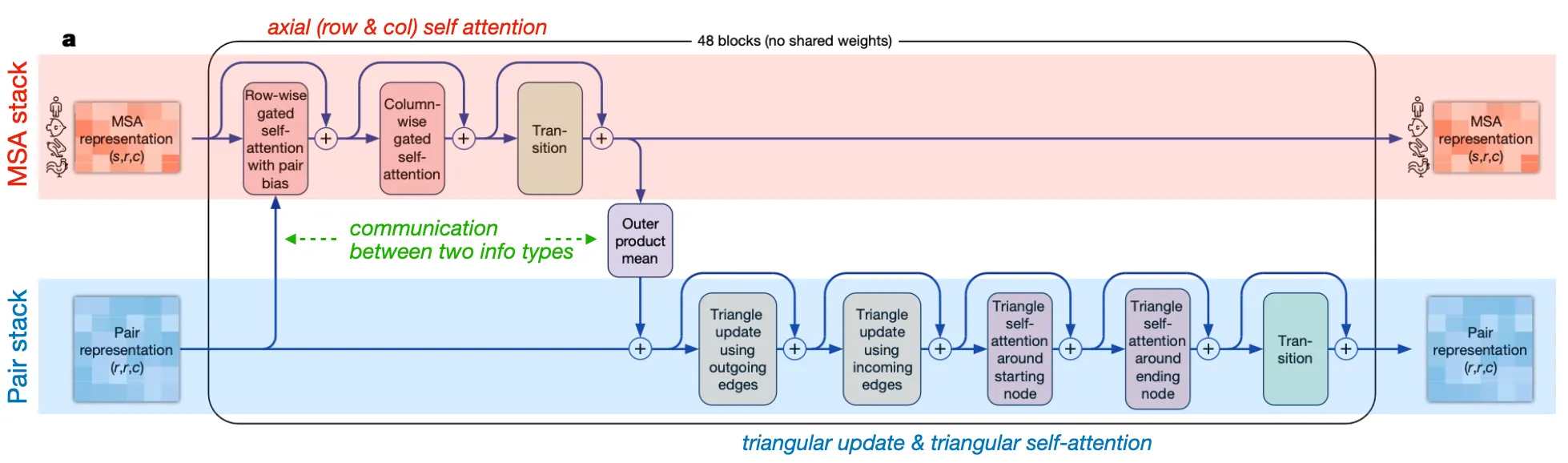
Evoformer stack

Input: MSA representation & Pair representation (+ recycled input) Output: (updated) MSA representation & (updated) Pair representation Goal: Efficiently exchange and evolve information between MSA rep & pair rep
Two major stacks and their communication
β€’
MSA stack: update MSA embedding with Pair info
Axial (row-wise & column-wise) gated self-attention
β€’
Pair stack: update residue pair embedding with MSA info
Triangular operations
β€’
Communication (information exchange) between two stacks
β—¦
Attention biasing in row-wise gated self-attention: Pair info β†’ MSA rep
Why the pair bias is added at row-wise axial attention (not column-wise)?
Answer: Because of the shape of the two tensors match at row-wise axial attention.
β—¦
Outer product mean: MSA info β†’ Pair rep
details of outer product mean
Why outer product mean? And is it novel in AF2?
Answer: 1. Outer product may capture covarying information between two residues. We want to know some information (e.g. if residue ii has a mutation, does residue jj also have a mutation?) Also, outer product mean naturally forms equal shape with Pair representation.
2. No, outer product mean operation was already used in previous works (e.g. rawMSA, CopulaNet).
Spoiler!
In AF-Multimer, outer product mean operation is moved to the front.

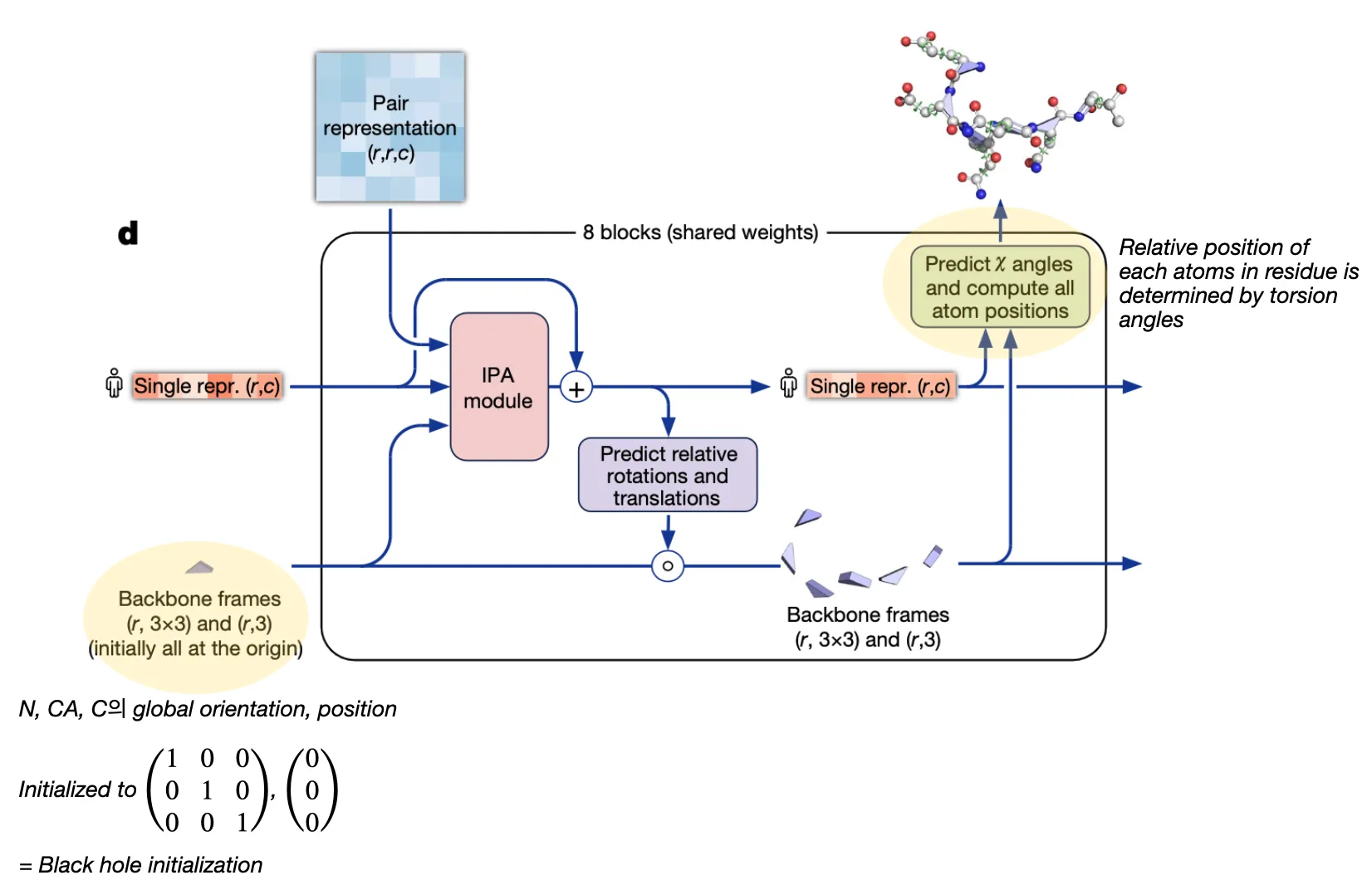
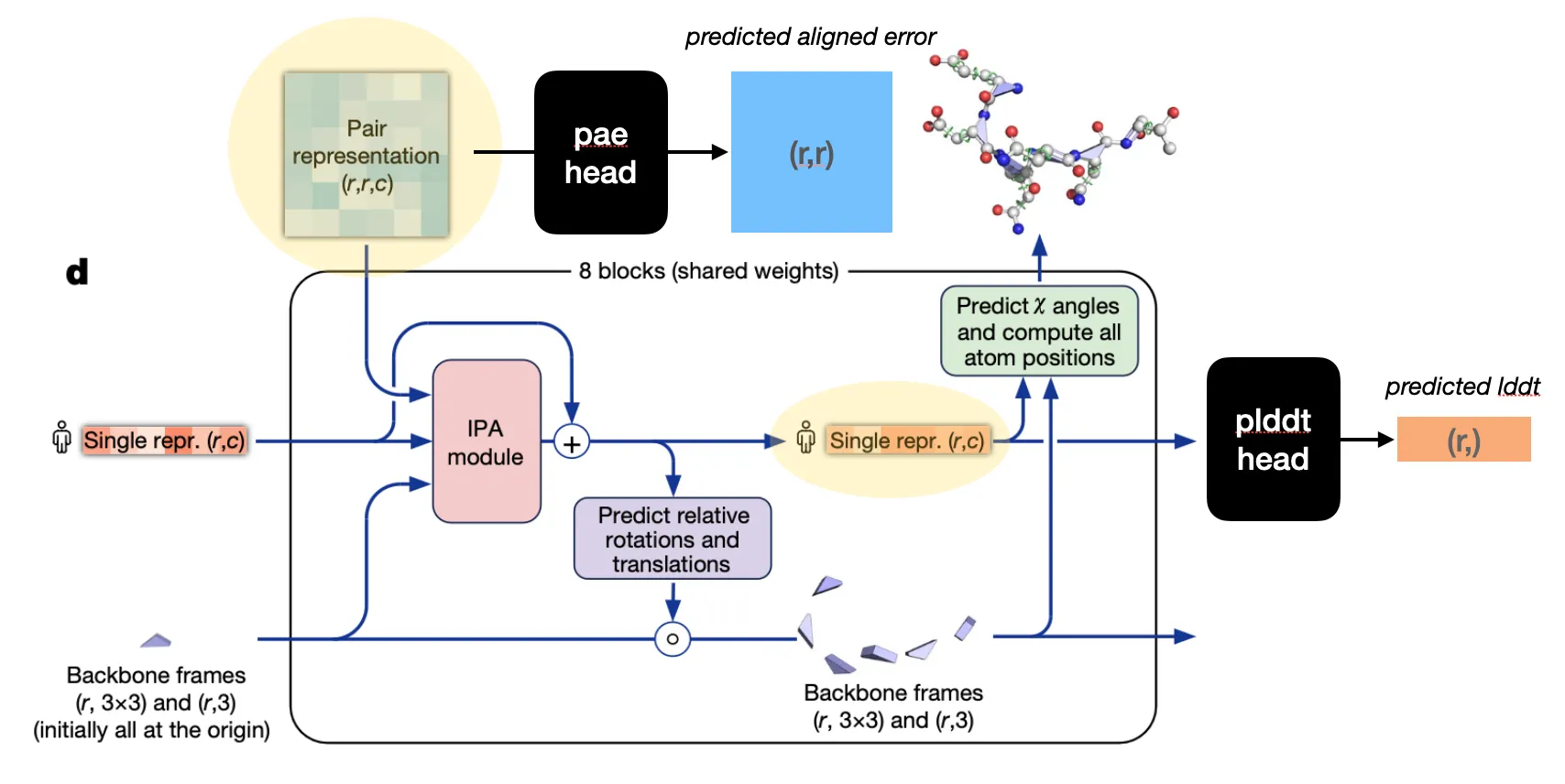
Structure module

Input: Pair representation & (previous) Single representation from Evoformer & (previous) backbone frames Output: (updated) Single representation & (updated) backbone frames Goal: Translate evoformer outputs into 3D coordinates Structure module is equivariant to rigid motions (translation, rotation)
Β Reminder
Single representation is the first row of MSA representation (i.e. query sequence representation).
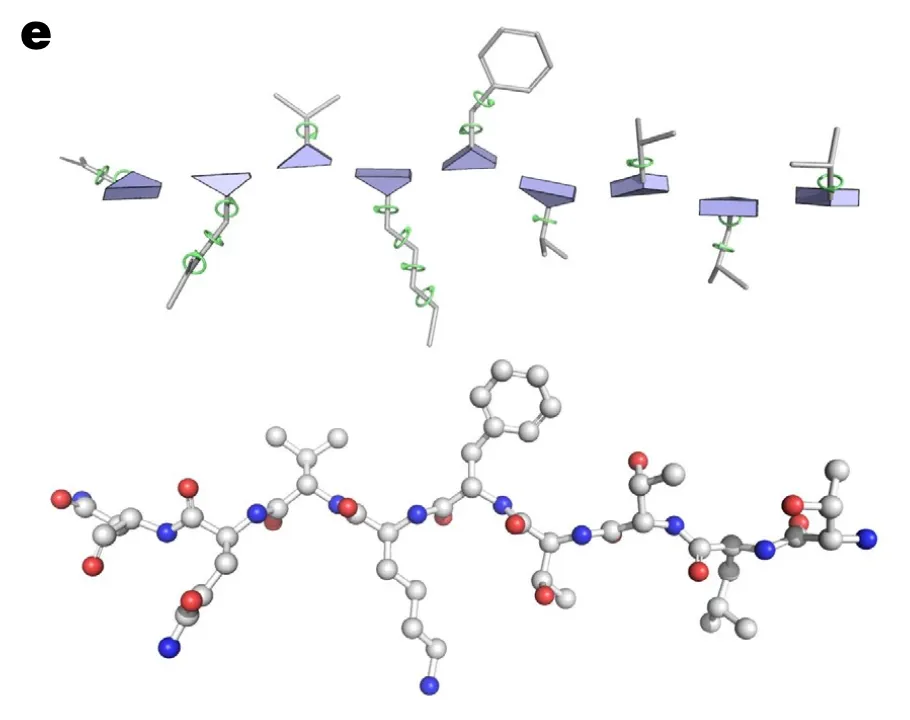
Residue representation
In AF2, each residue is represented as β€œresidue gas” and β€œΟ‡\chi angles”.
β€’
Residue gas (frame): blue triangle of N, CA, C (rigid backbone atoms)
β€’
Ο‡\chi angles: green circles (for side chain atoms)
So the structure module can be divided into two steps. It first predicts the position of residue gas, and then predicts Ο‡\chi angles!
Why only predict torsion angles? What about bond angles and bond lengths?
Two-step procedure
1. Residue backbone position prediction
2. Torsion angle prediction (followed by sidechain atom position determination)
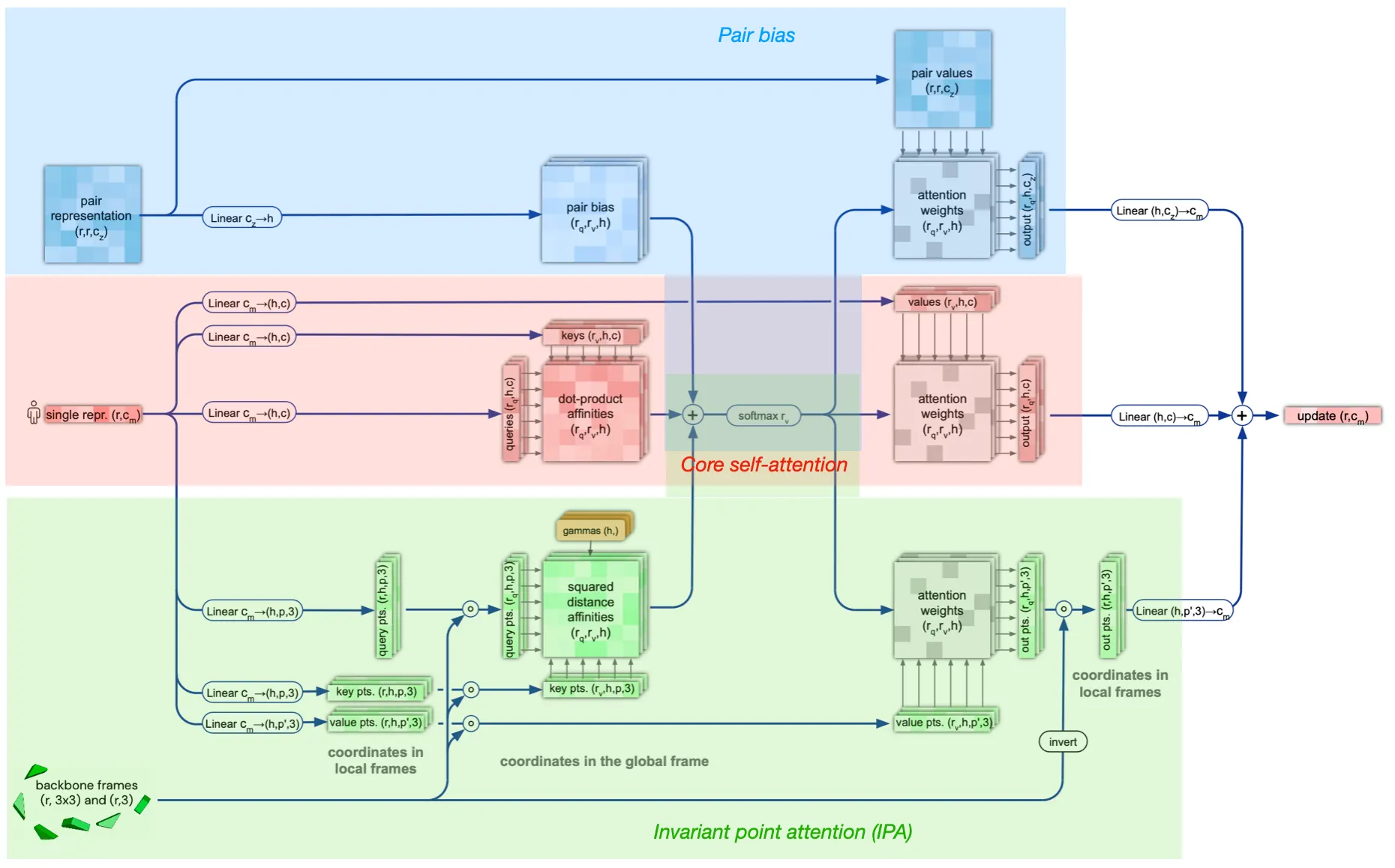
Structure module structure
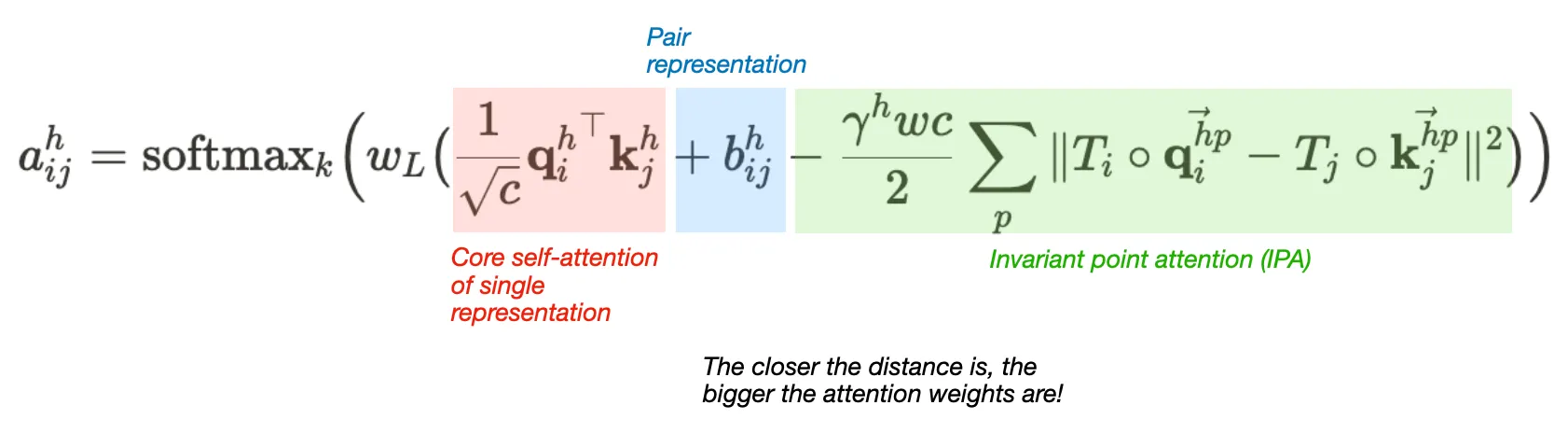
Attention between two residues on 3D space that is invariant to global transformations
aijh=softmaxk(wL(1cqih⊀kjh+bijhβˆ’Ξ³hwc2βˆ‘pβˆ₯Ti∘qihpβƒ—βˆ’Tj∘kjhpβƒ—βˆ₯2))a^h_{ij} = \text{softmax}_k \Big(w_L \big(\frac{1}{\sqrt{c}} {\mathbf{q}^h_i}^\top \mathbf{k}^h_j + b^h_{ij} - \frac{\gamma^h w c}{2} \sum_p \|T_i \circ \vec{\mathbf{q}^{hp}_i} - T_j \circ \vec{\mathbf{k}^{hp}_j}\|^2 \big) \Big)
Β Looks too complicated Let’s break down into three components!
β€’
Components
1. Core self-attention for Single representation
2. Pair representation (as bias term)
3. Invariant point attention (IPA) module
Pew.. To summarize,
Structure module algorithm
Is the IPA module invariant to translation and rotation?
Answer: Yes, since the rigid motions (tr, rot) cancels out in IPA algorithm. The IPA module performs tr&rot-invariant (not reflection) attention operations.
IPA algorithm and proof of its invariance

Additional inputs

Template pair stack
β€’
Pairwise template features are linearly projected to build initial template representation tstij\mathbf{t}_{s_tij}.
β€’
Each template representation is independently processed with template pair stack.
β€’
Output representations are aggregated by template point-wise attention.
β€’
The outputs are added to the Pair representations zij\mathbf{z}_{ij}.
Template pair stack algorithm
Template pointwise attention algorithm
Extra-MSA stack
β€’
Main MSA feature is built from the cluster center sequences. Other (sequences not selected as cluster center) MSA sequences are built into extra MSA feature by Extra-MSA stack.
β€’
This stack is relatively simple to embed more MSA results.
Extra MSA stack algorithm

Confidence module

Input: Pair representation (for PAE head) or Single representation (for pLDDT head) Output: Self-estimates of confidence score Goal: Provide the metrics to select the best structure
Confidence metrics in AF2: pLDDT, PAE, pTM
pLDDT head: predicts per-residue local confidence
PAE head: predicts per-(residue pair) confidence score
pTM: global confidence measure (calculated with PAE logit matrix)
Why all regression tasks in AF2 (plddt, pae, distogram) are transformed into classification task (by binning)?
Answer: (the authors did not mention any reasons for the transformation) Presumably the reason might be..
β€’
cross entropy loss is more stable than the L2 loss
β€’
classification is relatively robust to outliers (the first and last bin can cover outliers)

Loss

AF2 designed and adopted various losses to train the model.
Main FAPE loss + a number of auxiliary losses
LFAPE\mathcal{L}_{\text{FAPE}}: FAPE (Frame Aligned Point Error) loss
Laux\mathcal{L}_{\text{aux}}: Auxiliary loss (intermediate FAPE loss)
Ldist\mathcal{L}_{\text{dist}}: Distogram loss
Lmsa\mathcal{L}_{\text{msa}}: MSA loss
Lconf\mathcal{L}_{\text{conf}}: Confidence loss
LexpΒ resolved\mathcal{L}_{\text{exp resolved}}: Experimentally resolved loss
Lviol\mathcal{L}_{\text{viol}}: Violation loss

Recycling

Repeat the prediction process with Evoformer output & Structure module output
β€’
Gradients of the intermediate outputs are stopped. Only the last gradients are backpropagated.
β€’
Advantages
β—¦
Recycling deepens the network
β—¦
Model can experience various versions of input features for a single input sequence
β€’
When training,
Nβ€²=Uniform(1,Ncycle)N' = \text{Uniform}(1, N_{cycle})
Backpropagation is only performed for the last cycle (Nβ€²N'-th cycle).
β€’
When inference,
Nβ€²=NcycleN' = N_{cycle}
Why not always NcycleN_{cycle} during training?
Answer:
1.
To improve efficiency. The average number of cycle is Ncycle+12\frac{N_{\text{cycle}} + 1}{2}.
2.
Also act as auxiliary loss (requiring to provide plausible outputs mid-way through the inference)

Engineering

training protocol
self-distillation
optimization details
parameter initialization
loss clamping
reducing memory consumption
ablation studies

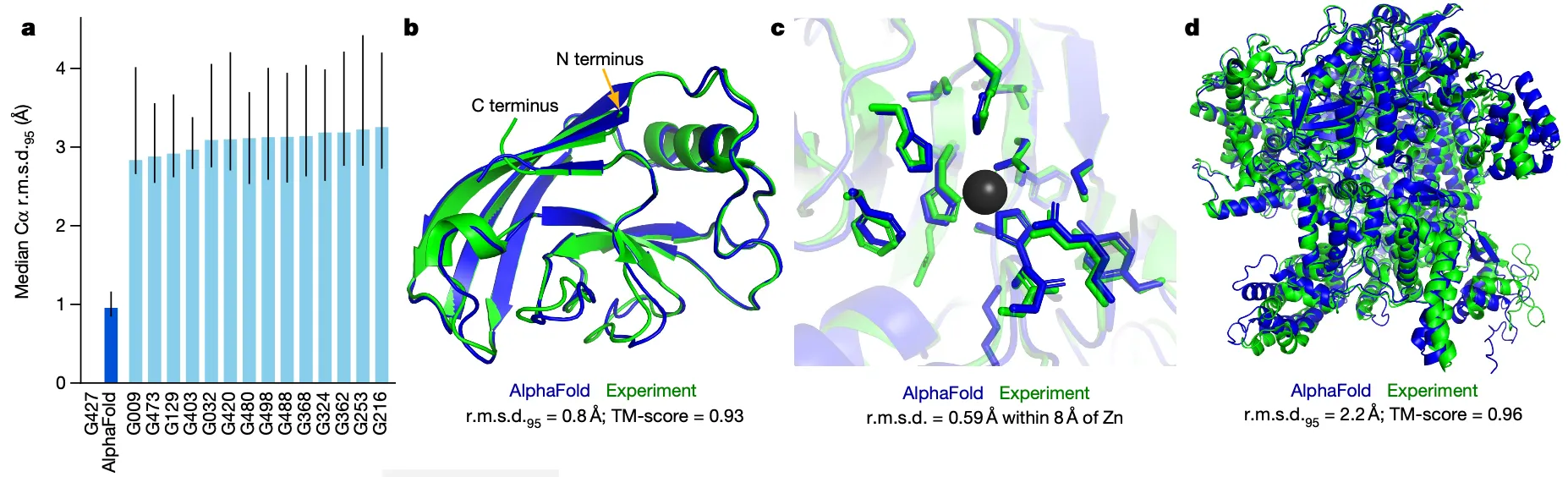
Results

Discussion

β€’
AF2 opened up the possibility of predicting protein structure at the proteome-scale
β€’
Major limitations
β—¦
AF2 relies quite heavily on MSA & known structure info
β†’ may not work well for point mutations and antibodies
β—¦
AF2 only predicts single chain structure
β†’ but most functional studies require multi-chain structural relationships
e.g. 6P9X
β—¦
High memory consumption
Triangular operations consists of (Nres3,Nhead)(N_{\text{res}}^3, N_{\text{head}}) floating point numbers

Reference